Existe una verdad fundamental en el arte de la pedagogía, un secreto que todo gran maestro conoce. El aprendizaje no florece en la comodidad de lo ya sabido, ni se marchita en la desesperación de lo imposible. Germina en un terreno fértil y desafiante, en la frontera precisa que separa la competencia actual de la maestría futura. Es una zona de esfuerzo productivo, un espacio donde la incertidumbre y el potencial coexisten en un delicado equilibrio. Durante generaciones, los educadores han perfeccionado la intuición para guiar a sus estudiantes hacia esta frontera, calibrando la dificultad de cada lección para maximizar el crecimiento. Ahora, en la vanguardia de la inteligencia artificial, un equipo de investigadores ha logrado traducir esta sabiduría ancestral en un algoritmo. Han diseñado, en esencia, al maestro perfecto para las mentes digitales más avanzadas de nuestro tiempo.
Este desafío pedagógico se ha vuelto crucial en la era de los grandes modelos de lenguaje, o LLM por sus siglas en inglés. Estas arquitecturas de inteligencia artificial son estudiantes prodigiosos, dotados de un conocimiento enciclopédico extraído de vastas extensiones de texto y datos. Sin embargo, poseer información no es sinónimo de saber razonar. Para que estos modelos trasciendan la mera repetición y se adentren en la resolución de problemas complejos, necesitan un entrenamiento que se asemeje más a una tutoría socrática que a una memorización masiva. El método predilecto para esta instrucción es el aprendizaje por refuerzo, una técnica que emula el aprendizaje humano a través del ensayo y el error. El modelo intenta resolver un problema, recibe una recompensa si acierta y una penalización si falla, y ajusta sus conexiones internas para mejorar en el siguiente intento.
Para organizar esta práctica, los ingenieros de IA han adoptado una estrategia llamada aprendizaje curricular, que no es otra cosa que la versión digital de un plan de estudios. La idea, intuitiva y lógica, es presentar los problemas en un orden de dificultad creciente, empezando por los conceptos básicos para luego avanzar hacia los más complejos. Pero este enfoque, tan eficaz en la educación humana, tropieza con un obstáculo fundamental en el vertiginoso mundo del aprendizaje automático: la dificultad no es una propiedad estática de un problema, sino una relación dinámica entre el problema y quien aprende. Un desafío que hoy parece insuperable para un modelo de IA, mañana podría ser trivial.
Aquí es donde emerge una nueva y revolucionaria propuesta, detallada en un trabajo de investigación titulado VCRL, acrónimo de Aprendizaje por Refuerzo Curricular Basado en la Varianza. Sus autores, un grupo de científicos de Alibaba Cloud Computing, proponen un cambio de paradigma. En lugar de depender de un plan de estudios fijo, han desarrollado un método que permite al sistema de entrenamiento identificar dinámicamente el problema perfecto para el modelo en cada instante de su aprendizaje. ¿Y cómo lo logran? Mediante una idea de una elegancia y simplicidad asombrosas: han enseñado a la máquina a escuchar sus propias dudas. El sistema mide la «vacilación» o la incertidumbre del modelo frente a una tarea, y esta medida, capturada por una simple herramienta estadística llamada varianza, se convierte en la brújula que guía todo el proceso educativo. VCRL no impone un camino, sino que ilumina el siguiente paso más productivo, creando un tutor algorítmico personalizado que se adapta y evoluciona en perfecta sincronía con su pupilo digital.
El arte de enseñar a una inteligencia artificial a pensar
Para comprender la magnitud de este avance, es necesario adentrarse en el fascinante proceso mediante el cual las inteligencias artificiales modernas están aprendiendo a «pensar». Los modelos de lenguaje de última generación ya no se limitan a predecir la siguiente palabra en una frase. Se les está entrenando para emular el razonamiento humano en tareas que requieren lógica, planificación y una secuencia de pasos interconectados. Este proceso se conoce como «cadena de pensamiento» o Chain-of-Thought. En lugar de ofrecer una respuesta directa y a menudo opaca, se alienta al modelo a verbalizar su proceso deductivo, a «mostrar su trabajo» de la misma manera que lo haría un estudiante de matemáticas al resolver una ecuación compleja. Esta capacidad es fundamental para abordar problemas avanzados en campos como la ciencia, la programación y, de manera muy especial, las matemáticas, el campo de pruebas elegido por los creadores de VCRL.
El gimnasio donde estos modelos ejercitan sus músculos racionales se rige por un protocolo específico conocido como Aprendizaje por Refuerzo con Recompensas Verificables (RLVR). El proceso es metódico y riguroso. Imaginemos a un arquero entrenando para una competición. Para cada problema o «pregunta» que se le presenta al modelo, este no genera una única respuesta, sino un conjunto de ellas, normalmente dieciséis intentos distintos. Cada uno de estos intentos es una «trayectoria» o «rollout», una cadena de pensamiento completa que conduce a una solución. A continuación, entra en escena un «verificador», un juez infalible que no evalúa la elegancia del proceso, sino únicamente el resultado final. Este verificador otorga una recompensa binaria y austera: un ‘1’ si la respuesta es correcta, un ‘0’ si es incorrecta. No hay puntos por el esfuerzo ni calificaciones intermedias. Es un sistema de retroalimentación implacable que, a través de miles de repeticiones, permite al modelo aprender qué secuencias de razonamiento conducen al éxito y cuáles al fracaso.
Este es el motor del aprendizaje. Los algoritmos de refuerzo existentes, como el conocido Group Relative Policy Optimization (GRPO), funcionan sobre esta base. GRPO analiza el grupo de dieciséis respuestas generadas para una misma pregunta y aprende comparando las trayectorias exitosas con las fallidas. El sistema refuerza las conexiones neuronales que llevaron a las respuestas correctas y debilita las que condujeron a errores. De esta forma, el modelo expande continuamente las fronteras de su capacidad, explorando nuevas formas de razonar y consolidando las que demuestran ser efectivas. Este es el estado del arte, la tecnología fundamental sobre la cual VCRL se construye para dar un salto cualitativo.
El problema de la talla única en el aprendizaje automático
A pesar de su eficacia, el método de entrenamiento estándar adolece de una ineficiencia fundamental, una que cualquier educador reconocería de inmediato. El proceso se asemeja a entregarle al estudiante de IA un gigantesco libro de texto con miles de ejercicios ordenados al azar. El modelo dedica una inmensa cantidad de tiempo y recursos computacionales a dos tipos de tareas completamente improductivas. Por un lado, se enfrenta a problemas que son demasiado fáciles, aquellos que ya domina a la perfección. Resolverlos una y otra vez es como pedirle a un matemático que practique sumas de dos cifras; no ofrece ningún conocimiento nuevo, ninguna oportunidad de crecimiento. Es un desperdicio de energía.
Por otro lado, el modelo se topa con problemas que son abrumadoramente difíciles, desafíos que están tan por encima de su nivel de competencia actual que cualquier intento está condenado al fracaso. En esta situación, el modelo no obtiene ninguna señal de aprendizaje útil. Todas sus respuestas son incorrectas, y la retroalimentación es un monótono flujo de ceros. No hay un punto de apoyo, ninguna pista sobre cómo podría haberlo hecho mejor. Es el equivalente a pedirle a un estudiante de primaria que demuestre el último teorema de Fermat. El resultado no es aprendizaje, sino frustración computacional.
La solución que primero viene a la mente es la que la pedagogía humana ha empleado durante siglos: un currículo ordenado. ¿Por qué no clasificar todos los problemas de antemano, desde los más sencillos hasta los más complejos, y presentárselos al modelo en esa secuencia lógica? Esta estrategia, sin embargo, se desmorona ante la naturaleza dinámica del aprendizaje de la IA. El error fundamental de un currículo estático radica en suponer que la dificultad es una propiedad inherente y fija de un problema. No lo es. La dificultad es una medida relativa, una danza entre el desafío y la habilidad del aprendiz.
Un problema que es moderadamente difícil para un modelo en la primera hora de entrenamiento puede volverse trivial después de mil pasos de optimización. A medida que el modelo aprende y sus parámetros internos se actualizan, su percepción de la dificultad del mundo cambia. Un currículo predefinido se vuelve obsoleto casi al instante. Lo que se necesita no es un mapa fijo, sino una brújula que funcione en tiempo real, un indicador que pueda decirnos, en cualquier momento, qué problema representa el desafío perfecto para el estado actual y en constante evolución del modelo. La búsqueda de esta brújula es la motivación central detrás de la investigación de VCRL.
La varianza como brújula de la dificultad
La solución propuesta por los investigadores es de una brillantez conceptual que reside en su simplicidad. En lugar de buscar complejos indicadores externos de dificultad, encontraron la señal perfecta en el propio comportamiento del modelo. La clave, descubrieron, está en la varianza de las recompensas obtenidas en el grupo de respuestas. La varianza, en estadística, es una medida de la dispersión de un conjunto de datos respecto a su media. En este contexto, se convierte en una brújula infalible para medir la dificultad de una tarea para el estado actual del modelo.
El razonamiento es el siguiente. Consideremos los dos extremos improductivos del aprendizaje. Cuando un problema es trivialmente fácil para el modelo, casi todos sus dieciséis intentos serán correctos. El conjunto de recompensas será algo parecido a {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}. La media de estas recompensas es 1, y la dispersión de los datos en torno a esa media es nula. La varianza es 0. El modelo no está aprendiendo nada nuevo; está simplemente confirmando lo que ya sabe.
Ahora, consideremos el caso opuesto: un problema imposiblemente difícil. Todos los intentos del modelo fracasarán. El conjunto de recompensas será {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}. La media es 0, y de nuevo, no hay dispersión alguna. La varianza es también 0. El modelo está completamente perdido, sin ninguna retroalimentación positiva que le indique un camino a seguir. En ambos escenarios, una varianza de cero es una señal inequívoca de que el aprendizaje está estancado.
La oportunidad de oro para el aprendizaje, el punto de máximo crecimiento, surge precisamente en el medio. Ocurre cuando el modelo se encuentra en un estado de máxima incertidumbre, cuando el problema está justo en el límite de su capacidad. En esta situación, aproximadamente la mitad de sus intentos tendrán éxito y la otra mitad fracasarán. El conjunto de recompensas podría parecerse a {1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0}. Aquí, los datos están lo más dispersos posible. La varianza de las recompensas alcanza su valor matemático máximo. Este pico en la varianza es una señal clara y potente. Le dice al sistema de entrenamiento: «Este problema es perfecto. No es demasiado fácil, no es demasiado difícil. Es el desafío justo que necesito para aprender y mejorar».
Lo que VCRL logra es más que una simple optimización técnica; es la encarnación algorítmica de un principio pedagógico fundamental conocido como la «zona de desarrollo próximo», un concepto acuñado por el psicólogo Lev Vygotsky. Esta zona describe el espacio entre lo que un aprendiz puede hacer sin ayuda y lo que puede lograr con la guía de un mentor. Es la zona del «desafío óptimo». Los maestros humanos buscan intuitivamente esta zona mediante la observación y la interacción. Evalúan el desempeño de un estudiante y le proponen tareas que estiran sus habilidades sin quebrar su confianza.
VCRL automatiza este proceso de búsqueda de la «zona Ricitos de Oro»: el problema que no es ni demasiado fácil ni demasiado difícil, sino perfecto. Reemplaza la intuición del maestro por una métrica precisa y cuantificable: la varianza de la recompensa. Es el propio desempeño del modelo en una tarea lo que genera la señal que le dice al «maestro» algorítmico si la tarea es apropiada. Esto crea un tutor perpetuamente adaptativo y perfectamente personalizado. A diferencia de un currículo estático, la métrica de dificultad de VCRL se genera a partir de la interacción del modelo con el problema mismo, asegurando que el plan de estudios evolucione en perfecta sintonía con la creciente competencia del modelo. Es un cambio fundamental desde las rutas de aprendizaje preprogramadas hacia un aprendizaje autodirigido y guiado dinámicamente.
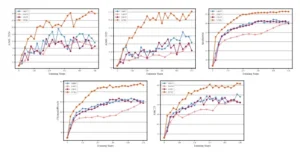
Curva de rendimiento de Qwen3-4B-Base en los cinco puntos de referencia utilizando varios métodos de RL a lo largo de los pasos de entrenamiento.

Curva de rendimiento de Qwen3-8B-Base en los cinco puntos de referencia utilizando varios métodos de aprendizaje automático (RL) a lo largo de los pasos de entrenamiento.
VCRL, una estrategia de entrenamiento a medida
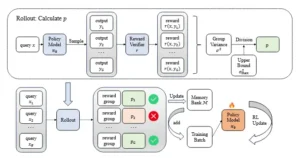
El marco de VCRL se materializa a través de dos mecanismos ingeniosamente interconectados, diseñados para seleccionar los problemas más valiosos y asegurar que se utilicen de la manera más eficiente posible. El proceso, ilustrado en el diagrama del artículo científico, puede entenderse como una sofisticada cadena de montaje para la creación de lotes de entrenamiento de alta calidad.
El primer componente es el Muestreo Dinámico Basado en la Varianza. Esta es la fase de «selección» o el filtro de calidad del sistema. Para cada lote de problemas potenciales extraídos del conjunto de datos de entrenamiento, el sistema realiza la serie de intentos o «rollouts». A continuación, calcula la varianza de las recompensas para cada problema y la normaliza para obtener un valor, denominado p, que va de 0 a 1. Este valor p es la puntuación de «valor pedagógico» del problema. El sistema actúa entonces como un portero selectivo. Aquellos problemas con un valor p bajo, es decir, con baja varianza, son descartados. Estos son los problemas triviales y los imposibles, el ruido que obstaculiza el aprendizaje eficiente. Solo los problemas con un valor p alto, aquellos que generaron una alta varianza, son seleccionados para formar parte del lote de entrenamiento que se utilizará para actualizar el modelo.
El segundo componente es el Aprendizaje por Repetición con un Banco de Memoria. Este es el mecanismo de «eficiencia y refuerzo». Los investigadores se dieron cuenta de que realizar «rollouts» constantemente para cada problema solo para decidir si es valioso o no, es un proceso computacionalmente muy costoso. Para solucionar esto, VCRL incorpora un «banco de memoria». Este banco no es más que una biblioteca cuidadosamente curada de problemas «dorados», aquellos que en el pasado demostraron tener una alta varianza y, por lo tanto, un alto valor pedagógico. El sistema funciona de la siguiente manera: cuando el filtro de muestreo dinámico descarta un problema de bajo valor de un nuevo lote, deja un hueco. Para llenar ese vacío y mantener el tamaño del lote constante, el sistema no toma otro problema al azar, sino que recurre a su banco de memoria y extrae uno de los problemas de alto valor previamente identificados. De esta forma, se asegura de que cada lote de entrenamiento esté saturado de tareas óptimamente difíciles, maximizando el valor de cada ciclo de actualización.
Estos dos componentes no son simplemente aditivos; su relación es profundamente sinérgica. Uno se encarga de encontrar el material valioso, y el otro garantiza que ese material se utilice de manera eficiente y repetida, creando un poderoso ciclo de retroalimentación positiva que acelera el aprendizaje. El Muestreo Dinámico actúa como un «prospector», cribando montañas de datos en busca de pepitas de oro, que son los problemas de alta varianza. Es una actividad de alto esfuerzo pero de alta recompensa. El Aprendizaje por Repetición, con su banco de memoria, funciona como una «bóveda y refinería». Almacena estas pepitas de oro, evitando que el valioso descubrimiento sea un evento de una sola vez. Luego, las reintroduce en el proceso de entrenamiento, amortizando el coste computacional del descubrimiento inicial a lo largo de muchos pasos de aprendizaje.
Esta sinergia aborda directamente uno de los dilemas centrales del aprendizaje automático: el equilibrio entre la exploración (encontrar nuevos datos valiosos) y la explotación (aprender de los datos valiosos ya conocidos). El Muestreo Dinámico se encarga de la exploración, mientras que el banco de memoria perfecciona la explotación. El estudio de ablación presentado en el artículo científico demuestra empíricamente esta sinergia. Los resultados muestran que, partiendo de un modelo base, la adición del Muestreo Dinámico mejora el rendimiento, pero es la posterior inclusión del Aprendizaje por Repetición lo que proporciona el mayor salto de rendimiento marginal. Esto confirma el papel crucial del banco de memoria a la hora de amplificar los beneficios del muestreo dinámico, creando una arquitectura de aprendizaje que no solo es más inteligente, sino también mucho más eficiente.
La prueba de fuego: VCRL en el campo de batalla matemático
Una nueva metodología de enseñanza, por muy elegante que sea su teoría, debe demostrar su valía en la práctica. Para ello, los investigadores sometieron a los modelos entrenados con VCRL a una serie de pruebas de razonamiento matemático extremadamente exigentes. En esencia, organizaron una competición académica de alto nivel, enfrentando su nuevo método de «tutoría» algorítmica contra las técnicas de entrenamiento existentes. Los campos de batalla fueron cinco bancos de pruebas reconocidos, incluyendo conjuntos de datos con problemas de nivel de olimpiada matemática como AIME y OlympiadBench.
Los resultados, presentados con claridad en las tablas del estudio, constituyeron una victoria decisiva y contundente para VCRL. En dos modelos de diferentes tamaños (Qwen3-4B y Qwen3-8B) y en los cinco bancos de pruebas, VCRL superó de manera consistente y significativa a todas las alternativas. No solo mejoró drásticamente el rendimiento del modelo base, sino que también dejó atrás a los modelos entrenados con los métodos de refuerzo más avanzados hasta la fecha, como GRPO, DAPO y GSPO. El salto de rendimiento fue especialmente notable en los conjuntos de datos más difíciles, aquellos que requieren cadenas de razonamiento largas y complejas, lo que sugiere que VCRL es excepcionalmente bueno para desbloquear las capacidades de razonamiento profundo de los modelos.
Para ilustrar la magnitud de la mejora, la siguiente tabla resume los resultados más destacados para el modelo más grande, Qwen3-8B, en algunos de los bancos de pruebas clave.
Rendimiento en pruebas de razonamiento matemático (Modelo Qwen3-8B)
| Método | AIME-2024 (Puntuación) | MATH500 (Puntuación) | Promedio General (Puntuación) |
| Modelo Base | 10.83 | 68.75 | 32.96 |
| + GRPO | 23.13 | 86.94 | 50.25 |
| + GSPO | 27.29 | 89.23 | 53.09 |
| + VCRL | 34.38 | 91.99 | 57.76 |
Los números hablan por sí solos. VCRL no solo produce una mejora marginal, sino un salto cualitativo, traduciendo la afirmación central del artículo en una evidencia cuantitativa innegable y estableciendo su posición en la vanguardia de las técnicas de entrenamiento de IA.
Sin embargo, la superioridad de VCRL no reside únicamente en alcanzar una puntuación final más alta. Los datos sobre la dinámica del entrenamiento revelan una historia más profunda: VCRL fomenta un proceso de aprendizaje fundamentalmente más sano, estable y exploratorio. Los modelos entrenados con este método no solo aprenden más rápido; se convierten en mejores «razonadores».
Los gráficos que muestran la evolución del rendimiento a lo largo de los pasos de entrenamiento revelan que la curva de VCRL no solo asciende más rápidamente, sino que también alcanza una meseta más alta que las de sus competidores. El análisis de las métricas internas del entrenamiento explica por qué. Una de las claves es la entropía. En los modelos de lenguaje, la entropía es una medida de la incertidumbre o la «creatividad» en sus generaciones. Mientras que otros métodos tienden a converger rápidamente hacia soluciones deterministas y repetitivas (lo que se refleja en una caída drástica de la entropía), VCRL mantiene un nivel de entropía saludable durante todo el proceso. El desafío constante y calibrado que VCRL presenta al modelo le obliga a seguir explorando una diversidad de caminos de razonamiento.
Esta exploración sostenida se traduce directamente en la generación de cadenas de pensamiento más largas y complejas. La métrica de «longitud de respuesta» muestra que los modelos VCRL aprenden a «pensar» más profundamente, desarrollando razonamientos más elaborados para resolver los desafiantes problemas que se les presentan. Además, el análisis de la norma del gradiente, una medida técnica de la magnitud de las actualizaciones del modelo, muestra que los ajustes de VCRL son más pequeños y estables. Al evitar los problemas excesivamente fáciles o difíciles, que pueden causar actualizaciones erráticas y desestabilizadoras, VCRL guía al modelo a lo largo de una trayectoria de optimización mucho más suave y productiva. No se trata solo de aprender más rápido, sino de aprender de una manera más inteligente y sólida.
Hacia un aprendizaje automático más humano e inteligente
La investigación detrás de VCRL representa mucho más que una simple mejora incremental en los algoritmos de entrenamiento de inteligencia artificial. Supone un paso significativo para alejarse de los enfoques de fuerza bruta computacional, que han dominado el campo durante años, y avanzar hacia un paradigma más matizado, eficiente e inteligente, inspirado directamente en los principios de la pedagogía humana. Al enseñar a las máquinas a aprender de su propia incertidumbre, hemos comenzado a dotarlas de una de las herramientas más poderosas del intelecto: la capacidad de reconocer los límites del propio conocimiento y utilizarlos como guía para el crecimiento.
Las implicaciones de este trabajo trascienden el ámbito técnico y se extienden a múltiples dominios. Desde una perspectiva científica y filosófica, VCRL tiende un puente entre el mundo estadístico del aprendizaje automático y la ciencia cognitiva del aprendizaje humano. Demuestra que conceptos que antes se consideraban abstractos o puramente psicológicos, como la «zona de desarrollo próximo», no solo son filosóficamente interesantes, sino que pueden ser traducidos a algoritmos matemáticos efectivos y rigurosos. Nos acerca a una comprensión más profunda de la naturaleza universal del aprendizaje, ya sea en un cerebro biológico o en un circuito de silicio.
En el plano tecnológico y económico, el inmenso coste asociado al entrenamiento de los modelos de IA de última generación se ha convertido en uno de los principales cuellos de botella para el progreso. Estos procesos consumen cantidades masivas de energía y recursos computacionales, limitando la investigación de vanguardia a un puñado de corporaciones y laboratorios con presupuestos multimillonarios. Al hacer que el proceso de entrenamiento sea significativamente más eficiente, VCRL y otros métodos similares tienen el potencial de democratizar el desarrollo de la IA. Podrían reducir la huella de carbono de los centros de datos, abaratar los costes de la investigación y, en última instancia, acelerar el ritmo de la innovación al permitir que más actores participen en la creación de la próxima generación de inteligencia artificial.
Mirando hacia el futuro, el principio fundamental de VCRL, que es utilizar la incertidumbre de un modelo como brújula para el aprendizaje, es una idea potente y generalizable. Aunque este estudio se centró en el razonamiento matemático, no hay ninguna razón para que este enfoque no pueda extenderse a otros dominios complejos. Podríamos imaginar sistemas de IA que aprenden a programar de manera más eficiente al enfrentarse a tareas de codificación que se encuentran justo en el límite de su habilidad, o modelos que ayudan en el descubrimiento científico al explorar hipótesis donde su confianza es más baja. Incluso podría aplicarse a las artes creativas, guiando a una IA a explorar estilos y composiciones que desafíen sus patrones establecidos. VCRL no es solo un algoritmo; es una filosofía de enseñanza para máquinas, una que nos encamina hacia un futuro con una inteligencia artificial que aprende de forma más robusta, más eficiente y, quizás, un poco más como nosotros.
Referencias
Jiang, G., Feng, W., Quan, G., Hao, C., Zhang, Y., Liu, G., & Wang, H. (2025). VCRL: Variance-based Curriculum Reinforcement Learning for Large Language Models. arXiv preprint arXiv:2509.19803.



