Vivimos en la era de la inteligencia artificial. Desde los algoritmos que recomiendan nuestra próxima serie favorita hasta los sistemas que diagnostican enfermedades con una precisión sobrehumana, la IA se ha tejido en el entramado de nuestra vida cotidiana. En el corazón de esta revolución se encuentran las redes neuronales convolucionales (CNNs), una clase de algoritmos inspirados en la corteza visual humana que han demostrado una capacidad casi mágica para reconocer patrones en datos complejos, especialmente en imágenes. Son las CNNs las que permiten a un coche autónomo distinguir a un peatón de una señal de tráfico, a un radiólogo detectar un tumor en una tomografía y a nuestros teléfonos organizar miles de fotos por rostros y lugares.
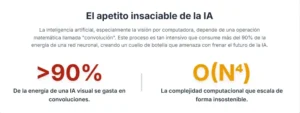
Sin embargo, esta proeza computacional tiene un coste oculto, uno que está creciendo a un ritmo alarmante y que amenaza con frenar el propio progreso que ha hecho posible. El motor de las CNNs es una operación matemática llamada convolución. En esencia, una convolución implica deslizar un pequeño filtro o «kernel» sobre una imagen, multiplicando y sumando valores en cada paso para extraer características fundamentales como bordes, texturas o formas. Este proceso, repetido millones de veces a través de múltiples capas, es lo que permite a la red «ver» y «entender». Pero es una operación de fuerza bruta, computacionalmente voraz. Se estima que más del 90% de la energía consumida y del tiempo de cálculo en una red neuronal convolucional se dedica exclusivamente a estas operaciones.
A medida que nuestras ambiciones para la IA crecen, también lo hace el tamaño y la complejidad de estas redes, y con ello, su insaciable sed de energía. Los centros de datos que albergan estos gigantes computacionales ya consumen una porción significativa de la electricidad mundial, una cifra que se proyecta que se dispare en los próximos años. Nos enfrentamos a un muro energético. La ley de Moore, la observación de que el número de transistores en un chip se duplica aproximadamente cada dos años, se está desacelerando. Las mejoras en la eficiencia de los chips electrónicos tradicionales, aunque impresionantes, ya no son suficientes para seguir el ritmo exponencial de las demandas de la IA. Si no encontramos una forma radicalmente nueva de realizar estos cálculos, corremos el riesgo de entrar en una «recesión de la IA», un futuro en el que nuestro progreso se vea limitado no por nuestra imaginación, sino por nuestra capacidad para alimentar nuestras creaciones.
Un nuevo y revolucionario estudio, titulado «Near-energy-free photonic Fourier transformation for convolution operation acceleration», presenta una solución tan elegante como radical a este inminente cuello de botella. Propone un cambio de paradigma: en lugar de forzar a los electrones a través de circuitos de silicio cada vez más densos, ¿por qué no utilizar la luz misma para realizar el trabajo pesado? Los investigadores han desarrollado un dispositivo fotónico en un chip, un correlacionador de transformación conjunta fotónica (pJTC), que aprovecha una peculiaridad fundamental de la física de la luz para realizar convoluciones de una manera drásticamente más eficiente.
La clave de su enfoque reside en un principio matemático conocido como el teorema de la convolución. Este teorema establece que una operación de convolución increíblemente compleja en el dominio espacial (el mundo de los píxeles tal como lo conocemos) se convierte en una simple multiplicación punto por punto en el «dominio de la frecuencia» o dominio de Fourier. El problema siempre ha sido que llegar a este dominio de Fourier, y volver de él, es en sí mismo un proceso computacionalmente costoso para la electrónica, a menudo anulando los beneficios. Pero aquí es donde la luz tiene un as en la manga: una simple lente realiza una transformación de Fourier de forma casi instantánea y, lo que es más importante, prácticamente sin consumir energía. Es una operación que la naturaleza le regala a la óptica.
El dispositivo pJTC miniaturiza este concepto en un chip de silicio, reemplazando las voluminosas lentes de cristal por «lentes de Fresnel» en chip y los datos de píxeles por haces de luz modulados. Al hacerlo, reduce la complejidad computacional de la convolución de forma drástica. Lo que en la electrónica tradicional escala de manera casi insostenible (con una complejidad de O(N⁴) o, en el mejor de los casos, O(N³)), en este sistema fotónico se reduce a una escala mucho más manejable de O(N²).
Los resultados son asombrosos. El prototipo no solo ha demostrado ser capaz de realizar transformaciones de Fourier y convoluciones funcionales, sino que ha alcanzado una precisión del 98% en una tarea de clasificación de imágenes estándar (el reconocimiento de dígitos manuscritos del conjunto de datos MNIST). Y lo que es más prometedor, las proyecciones para futuras versiones del chip, que utilizarían múltiples longitudes de onda de luz para procesar datos en paralelo (multiplexación por división de longitud de onda), apuntan a una eficiencia energética y una densidad computacional que dejan en la sombra a las GPUs más avanzadas de la actualidad. Hablamos de mejoras potenciales de hasta 100 veces en eficiencia energética.
Este artículo se sumergirá en el fascinante mundo de la computación fotónica, explicando de manera accesible los conceptos de convolución, la transformada de Fourier y cómo la luz puede ser domesticada para acelerar el corazón palpitante de la inteligencia artificial. Exploraremos el ingenioso diseño del pJTC, analizaremos sus prometedores resultados y reflexionaremos sobre las profundas implicaciones que esta tecnología podría tener para el futuro de la IA, desde dispositivos de borde ultraeficientes hasta la próxima generación de supercomputadoras en la nube. Es la historia de cómo una de las operaciones más fundamentales de la naturaleza, la difracción de la luz a través de una lente, podría ser la clave para desbloquear el futuro de la inteligencia artificial.
El motor de la visión: entendiendo la convolución
Para apreciar la magnitud del avance que representa el pJTC, primero debemos entender la operación que pretende revolucionar: la convolución. Aunque su nombre suena intimidante, el concepto es sorprendentemente intuitivo y se inspira directamente en cómo funciona nuestro propio sistema visual.
Imagina que eres un detective tratando de encontrar una huella dactilar específica en una gran superficie. No miras toda la superficie a la vez. En lugar de eso, tomas una lupa y la vas deslizando metódicamente por toda el área, sección por sección. En cada punto, comparas lo que ves a través de la lupa con la imagen mental de la huella que estás buscando. Cuando encuentras una coincidencia, tu cerebro se «activa».
Una red neuronal convolucional hace exactamente lo mismo con una imagen digital. La «lupa» del detective es el kernel o filtro. Un kernel no es más que una pequeña matriz de números (por ejemplo, de 3×3 o 5×5 píxeles). Esta pequeña matriz está diseñada para detectar una característica muy específica. Un kernel podría estar diseñado para detectar bordes verticales, otro para bordes horizontales, otro para una curva específica, y otro para un cierto tono de color.
El proceso de convolución consiste en «deslizar» este kernel sobre cada posible posición de la imagen de entrada. En cada posición, la red realiza una operación matemática simple: multiplica los valores de los píxeles del kernel por los valores de los píxeles de la imagen que están directamente debajo de él y luego suma todos los resultados. El resultado de esta suma es un único número que se coloca en una nueva imagen de salida, llamada «mapa de características». Si el área de la imagen debajo del kernel coincide fuertemente con la característica que el kernel está diseñado para detectar (por ejemplo, un borde vertical), el resultado de la suma será un número alto. Si no hay coincidencia, el resultado será un número bajo.
Al final de este proceso de deslizamiento, hemos transformado la imagen original en un mapa de características que resalta todas las ubicaciones donde se encontró la característica específica del kernel. Una CNN no utiliza un solo kernel, sino cientos o miles de ellos en cada capa. Una capa podría tener kernels para detectar bordes simples, la siguiente capa tomaría esos mapas de bordes y usaría sus propios kernels para detectar formas más complejas como círculos o cuadrados, la capa siguiente podría detectar ojos o narices, y así sucesivamente, hasta que una capa final pueda identificar un «rostro humano».
El problema es la escala de esta operación. Para una imagen de, digamos, 1000×1000 píxeles y un kernel de 5×5, hay casi un millón de posiciones en las que hay que colocar el kernel. En cada una de esas posiciones, hay que realizar 25 multiplicaciones y 25 sumas. Y esto es solo para un kernel. Multiplícalo por los cientos de kernels en cada una de las docenas de capas de una red moderna, y el número de operaciones se dispara a billones o trillones.
Esta es la razón por la que el entrenamiento y la ejecución de las CNNs requieren hardware tan especializado y potente como las Unidades de Procesamiento Gráfico (GPUs), que son esencialmente máquinas diseñadas para realizar miles de estas pequeñas operaciones de multiplicación y suma en paralelo. Han sido el pilar de la revolución de la IA, pero como hemos visto, su arquitectura basada en electrones se está acercando a sus límites físicos y energéticos. La convolución espacial, este método de «fuerza bruta» de deslizar y calcular, es el cuello de botella. Se necesitaba un atajo, y las matemáticas, junto con la física de la luz, lo tenían reservado.
El atajo mágico: la transformada de Fourier
La solución a la carga computacional de la convolución se encuentra en un cambio de perspectiva, una de las ideas más profundas y hermosas de las matemáticas: la transformada de Fourier. Nombrada en honor al matemático francés Jean-Baptiste Joseph Fourier, esta herramienta nos permite descomponer cualquier señal (ya sea una onda de sonido, una serie temporal financiera o, en nuestro caso, una imagen) en la suma de sus frecuencias constituyentes.
La idea puede parecer abstracta, pero la analogía del sonido es muy útil. Cuando escuchas un acorde tocado por una orquesta, tu oído percibe un sonido complejo y único. Sin embargo, ese sonido complejo es en realidad la suma de muchas ondas de sonido simples, de diferentes frecuencias, producidas por los violines, los violonchelos, las flautas, etc. Lo que hace la transformada de Fourier es actuar como un «prisma» matemático para el sonido: toma el acorde complejo y lo descompone, mostrándote exactamente qué «notas» (frecuencias) están presentes y con qué «volumen» (amplitud).
Una imagen también puede ser vista como una señal bidimensional. Las «frecuencias» en una imagen se corresponden con la rapidez con la que cambian los valores de los píxeles. Las áreas de cambio lento, como un cielo azul uniforme, corresponden a frecuencias bajas. Las áreas de cambio rápido, como los bordes afilados de un edificio o la textura de la tela, corresponden a frecuencias altas. La transformada de Fourier de una imagen, por lo tanto, no es una imagen de objetos, sino un mapa de sus frecuencias constituyentes. El centro de este mapa representa las frecuencias bajas, y a medida que nos alejamos del centro, representamos las frecuencias cada vez más altas.
Aquí es donde entra en juego el teorema de la convolución. Este teorema nos dice que la operación increíblemente costosa de convolución en el dominio espacial es matemáticamente equivalente a una operación mucho más simple en el dominio de la frecuencia: una multiplicación elemento por elemento.
El proceso, en teoría, sería el siguiente:
- Toma tu imagen de entrada y tu kernel.
- Calcula la transformada de Fourier de ambos para convertirlos en mapas de frecuencia.
- Multiplica estos dos mapas de frecuencia juntos, píxel por píxel.
- Calcula la transformada de Fourier inversa del resultado para volver al dominio espacial.
El resultado de este proceso es idéntico al que se obtendría con el laborioso método de deslizamiento del kernel. La complejidad computacional se reduce drásticamente. Sin embargo, para un ordenador electrónico, los pasos 1 y 4 (la transformada de Fourier y su inversa) no son gratuitos. El algoritmo más eficiente para ello, la Transformada Rápida de Fourier (FFT), tiene una complejidad de O(N² log N), que es mejor que la convolución de fuerza bruta, pero sigue siendo una carga significativa.
Pero la naturaleza nos ofrece una forma de realizar el paso 2 casi gratis. Como se mencionó, cualquier lente simple, ya sea el cristal de unas gafas o la lente de una cámara, realiza una transformada de Fourier óptica bidimensional en cualquier luz que la atraviese. La imagen que se forma en el punto focal de una lente es, literalmente, la descomposición en frecuencias de la imagen de entrada. Este fenómeno físico, conocido desde hace siglos, es la pieza central de la innovación del pJTC. Si podemos construir un sistema que utilice lentes en un chip para realizar estas transformadas, el cuello de botella computacional podría, en teoría, desaparecer.

La arquitectura de la luz: el correlacionador fotónico en un chip
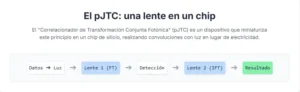
El desafío para los investigadores era tomar este principio óptico, tradicionalmente relegado a voluminosos sistemas de lentes en un banco de laboratorio (conocidos como sistemas 4F), y miniaturizarlo en un chip de silicio que pudiera fabricarse en masa, ser programable a alta velocidad y ser increíblemente eficiente energéticamente. El resultado es el correlacionador de transformación conjunta fotónica (pJTC).
La arquitectura del pJTC es una proeza de la nanoingeniería. A diferencia de un sistema 4F tradicional, donde la imagen y el filtro están separados, el pJTC se inspira en una arquitectura más simple y robusta llamada correlacionador de transformación conjunta. En este diseño, la señal de entrada (la imagen) y el kernel (el filtro) se colocan en el mismo plano de entrada. Esto simplifica enormemente el diseño y elimina la necesidad de componentes complejos de alineación y manipulación de fase.
El proceso dentro del chip funciona de la siguiente manera:
- Entrada y Modulación: La información, tanto de la imagen de entrada como del kernel, se codifica en haces de luz. Esto se hace utilizando una serie de diminutos moduladores de microdisco (MDMs). Un láser de onda continua fuera del chip envía luz al sistema, que se divide en múltiples canales. Cada canal pasa a través de un MDM. Aplicando un voltaje a un MDM, se puede cambiar su índice de refracción, lo que a su vez altera la cantidad de luz que deja pasar. De esta manera, el valor numérico de cada «píxel» de la entrada se traduce en una intensidad de luz correspondiente. Estos moduladores pueden operar a velocidades de gigahercios, millones de veces más rápido que los moduladores de luz espaciales utilizados en los sistemas ópticos tradicionales.
- Primera Transformada de Fourier: Los haces de luz modulados se guían a través de guías de onda de silicio hasta el plano focal de la primera lente de Fresnel en chip. Esta no es una lente curva tradicional, sino un patrón de difracción grabado en el silicio que imita la función de una lente. A medida que la luz combinada de la señal y el kernel pasa a través de esta lente, interfiere y se difracta, produciendo su transformada de Fourier combinada en el plano focal posterior.
- Detección y No Linealidad: En este plano de Fourier, una serie de fotodetectores (PDs) captura la intensidad del patrón de luz. Este es un paso crucial. Los fotodetectores son dispositivos de «ley cuadrática», lo que significa que su salida eléctrica es proporcional al cuadrado de la amplitud de la luz incidente (su intensidad). Esta operación no lineal es exactamente lo que se necesita para obtener los términos de correlación cruzada (que conducen a la convolución) y autocorrelación entre la señal y el kernel, tal como lo predice la matemática de la transformación conjunta.
- Segunda Transformada de Fourier: Las señales eléctricas de los fotodetectores se utilizan para controlar un segundo conjunto de moduladores. Estos modulan un nuevo conjunto de haces de luz, que luego pasan a través de una segunda lente de Fresnel en chip. Esta segunda etapa realiza la transformada de Fourier inversa, devolviendo la señal del dominio de la frecuencia al dominio espacial.
- Salida: El patrón de luz resultante es capturado por un segundo conjunto de fotodetectores, cuya salida eléctrica es el resultado final de la convolución entre la imagen de entrada original y el kernel.
Todo este proceso ocurre a la velocidad de la luz, con el consumo de energía concentrado principalmente en los moduladores y detectores, mientras que las transformadas de Fourier en sí mismas son pasivas y casi libres de energía. El chip fue fabricado utilizando los procesos estándar de la fotónica de silicio de AIM Photonics, lo que demuestra su viabilidad para la producción a gran escala.
Poniendo la luz a prueba: calibración y resultados
Un diseño teórico elegante es una cosa, pero hacerlo funcionar en el mundo real, con las imperfecciones inherentes a la fabricación a nanoescala, es otra muy distinta. Una parte crucial del estudio fue el riguroso proceso de prueba y calibración del prototipo de pJTC.
Las primeras mediciones confirmaron que los componentes individuales funcionaban según lo diseñado. Los moduladores de microdisco mostraron una alta relación de extinción (la diferencia entre el estado «encendido» y «apagado») y la capacidad de operar a velocidades de 1 GHz, con diagramas de ojo abiertos que indicaban una alta integridad de la señal. Las simulaciones de la lente de Fresnel en chip mostraron una focalización de la luz eficiente. El sistema demostró una notable estabilidad a largo plazo, manteniendo un rendimiento constante durante un período de prueba de 24 horas.
Sin embargo, al caracterizar el rendimiento de la transformación de Fourier del sistema completo, los investigadores encontraron una desviación entre la salida experimental y la transformada de Fourier ideal teórica. Este tipo de discrepancia es común en la fotónica integrada y puede ser causada por una variedad de factores, como limitaciones litográficas en la fabricación de la lente o variaciones minúsculas en el grosor del sustrato de silicio. Una de las principales fuentes de error identificadas fueron las diferencias submicrométricas en la longitud efectiva del camino óptico entre las diferentes guías de onda que llevan la luz a la lente.
Para corregir esto, los investigadores desarrollaron un ingenioso proceso de calibración única. Crearon un modelo matemático del sistema que incluía términos de fase ajustables para cada canal de entrada. Luego, recopilaron un conjunto de datos completo de pares de entrada-salida del chip real y utilizaron un algoritmo de optimización para encontrar los valores de fase que minimizaban la diferencia entre la salida del modelo y la salida experimental. Una vez que se determinan estas correcciones de fase estáticas, se pueden implementar en futuras versiones del chip utilizando cambiadores de fase fotónicos, componentes que pueden ajustar finamente el tiempo de viaje de la luz en cada guía de onda.
Los resultados de esta calibración fueron impresionantes. La salida corregida del chip se alineó casi perfectamente con la de una transformada de Fourier ideal. Esto demostró que, a pesar de las imperfecciones de fabricación, el sistema podía ser calibrado para lograr una alta fidelidad computacional.
Con el sistema calibrado, el siguiente paso fue probar su capacidad para una tarea de aprendizaje automático del mundo real. Utilizaron el pJTC para realizar la capa de convolución de una red neuronal entrenada para clasificar los dígitos manuscritos del famoso conjunto de datos MNIST. Crearon un modelo de emulación de software que capturaba con precisión el comportamiento del sistema electro-óptico, incluidas sus no idealidades. Entrenaron la red neuronal utilizando este modelo y luego evaluaron su rendimiento.
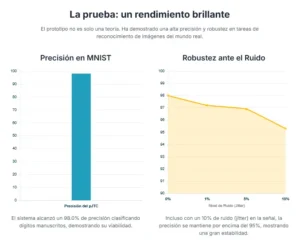
El pJTC alcanzó una precisión de clasificación del 98.0% en el conjunto de datos MNIST, un resultado excelente que demuestra la viabilidad del enfoque para tareas de inferencia de IA. Además, para probar la robustez del sistema, introdujeron deliberadamente un retardo temporal aleatorio (jitter) en las señales eléctricas de entrada, simulando las imperfecciones que podrían ocurrir en un sistema real de alta velocidad. Incluso con un retardo aleatorio del 10%, la precisión solo disminuyó al 95.3%, destacando la notable resistencia del sistema al ruido temporal.
El horizonte de la luz: escalabilidad y el futuro de la computación de IA
El prototipo demostrado es un primer paso monumental, pero el verdadero potencial del pJTC reside en su escalabilidad. El estudio concluye con una mirada hacia el futuro, proyectando el rendimiento de arquitecturas de pJTC más avanzadas y comparándolas con el estado del arte de la computación electrónica.
La clave para escalar el rendimiento es el paralelismo. La luz tiene una propiedad maravillosa: diferentes colores (longitudes de onda) pueden viajar a través de la misma guía de onda sin interferir entre sí. Esta técnica, conocida como multiplexación por división de longitud de onda (WDM), es la columna vertebral de la internet moderna, permitiendo que múltiples flujos de datos viajen a través de una sola fibra óptica.
Los investigadores proponen una arquitectura de pJTC mejorada que incorpora WDM. En este diseño, múltiples láseres de diferentes colores se integran en el chip, y cada color procesa un conjunto diferente de datos o kernels en paralelo a través de las mismas lentes. Esto multiplica la capacidad de cálculo del chip sin aumentar significativamente su tamaño.
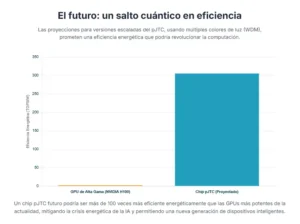
Las proyecciones de rendimiento para estos sistemas escalados son asombrosas. Un futuro chip pJTC, aprovechando la WDM y los procesos de fabricación de fundición disponibles actualmente, podría alcanzar una eficiencia energética de 305 TOPS/W (billones de operaciones por segundo por vatio) y una densidad computacional de 40.2 TOPS/mm².
Para poner estas cifras en perspectiva, la GPU H100 de NVIDIA, uno de los aceleradores de IA más potentes del mercado, ofrece alrededor de 2 TOPS/W. El pJTC promete una mejora de más de 100 veces en eficiencia energética. Esto no es una mejora incremental; es un salto de gigante. Un centro de datos equipado con este tipo de tecnología podría ofrecer la misma capacidad de cálculo que los centros de datos actuales, pero consumiendo una fracción minúscula de la energía. Alternativamente, podría ofrecer una capacidad de cálculo órdenes de magnitud mayor con el mismo consumo de energía.
Las implicaciones de este salto en eficiencia y densidad son profundas y de gran alcance. A nivel social y económico, podría mitigar la inminente crisis energética de la IA. Permitiría que el crecimiento de los servicios de IA continúe de manera sostenible, sin que el consumo de energía de los centros de datos se convierta en una carga insostenible para las redes eléctricas y el medio ambiente.
A nivel tecnológico, esta tecnología podría desbloquear capacidades de IA que actualmente son computacionalmente prohibitivas. Modelos de lenguaje más grandes y complejos, simulaciones científicas de mayor fidelidad y sistemas de visión por ordenador en tiempo real con una resolución sin precedentes podrían volverse factibles. En el borde de la red (edge computing), los chips pJTC podrían habilitar una nueva generación de dispositivos inteligentes y autónomos. Imagina gafas de realidad aumentada que puedan realizar un reconocimiento de escenas complejo en tiempo real, drones que puedan navegar de forma autónoma con un consumo de energía mínimo, o sensores médicos implantables que puedan analizar datos biométricos con redes neuronales sofisticadas, todo ello sin necesidad de una conexión constante a la nube.
Desde una perspectiva científica, el pJTC es un ejemplo brillante de cómo los principios fundamentales de la física pueden ser aprovechados para superar las limitaciones de nuestra tecnología actual. Es un recordatorio de que la computación no es un campo confinado al silicio y los electrones. El universo nos ofrece otros sustratos para el cálculo, y la luz, con su velocidad, paralelismo y eficiencia inherentes, es quizás el más prometedor de todos.
Por supuesto, el camino desde este prototipo hasta un producto comercial a gran escala todavía presenta desafíos de ingeniería significativos, como la integración de láseres en el chip, la optimización de las lentes y la mejora de la eficiencia de las conversiones óptico-eléctricas. Sin embargo, este trabajo proporciona una prueba de concepto inequívoca y un camino claro hacia adelante.
En conclusión, el correlacionador de transformación conjunta fotónica no es solo un chip ingenioso. Es un faro que ilumina una posible salida a la crisis energética que se cierne sobre la inteligencia artificial. Al recurrir a la elegancia de la óptica y a la potencia de la transformada de Fourier, los investigadores han demostrado que las operaciones más fundamentales de la naturaleza pueden ser la clave para impulsar la próxima ola de inteligencia artificial. Hemos pasado décadas enseñando a las máquinas a «ver» utilizando algoritmos inspirados en la biología; ahora, parece que el futuro de esa visión podría depender no de imitar el cerebro, sino de dominar la luz.
Referencias
Feldmann, J., et al. (2021). Parallel convolutional processing using an integrated photonic tensor core. Nature, 589(7840), 52–58.
Goodman, J. W. (1968). Introduction to Fourier Optics. McGraw-Hill.
LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
Miscuglio, M., et al. (2020). Massively parallel amplitude-only Fourier neural network. Optica, 7(12), 1812–1819.
Sze, V., Chen, Y.-H., Yang, T.-J., & Emer, J. S. (2017). Efficient processing of deep neural networks: A tutorial and survey. Proceedings of the IEEE, 105(12), 2295–2329.
Weaver, C. S., & Goodman, J. W. (1966). A technique for optically convolving two functions. Applied Optics, 5(7), 1248–1249.



