Por un instante proyectemos a través de nuestra imaginación que un sistema de inteligencia artificial, uno de esos modelos de lenguaje gigantes que hoy dominan los titulares, debe juzgar la calidad de un resumen de noticias. No se trata de generar una respuesta, sino de actuar como un crítico: leer un texto, compararlo con su fuente original y otorgar una puntuación entre uno y cinco. Este tipo de tarea, conocida como “modelo de lenguaje grande como juez” (LLM-as-a-judge), se ha convertido en una práctica cada vez más común en el desarrollo y evaluación de sistemas de generación de lenguaje. Es eficiente, escalable y, en muchos casos, sorprendentemente alineado con el juicio humano.
Pero hay un problema fundamental que rara vez se discute fuera de los círculos técnicos: ¿qué tan seguro está el modelo de su propia evaluación? ¿Puede distinguir entre una decisión clara y una ambigua? ¿Sabe cuándo está adivinando, cuándo está confundido o cuándo su juicio podría ser erróneo?
Hasta hace muy poco, la respuesta era, en esencia, no. Los modelos de lenguaje grandes (LLMs, por sus siglas en inglés) suelen entregar una puntuación única, sin ningún indicio de su grado de certeza. Es como si un médico dijera “usted tiene una enfermedad grave” sin explicar si ese diagnóstico se basa en pruebas concluyentes o en una corazonada. En contextos de alto riesgo, como la medicina, la justicia o la toma de decisiones financieras, esa falta de transparencia puede ser peligrosa.
Un nuevo estudio, titulado Analyzing Uncertainty of LLM-as-a-Judge: Interval Evaluations with Conformal Prediction, aborda precisamente este vacío. Sus autores proponen un marco riguroso, matemáticamente sólido y práctico para que los LLMs no solo emitan juicios, sino que también expresen su incertidumbre de forma cuantificable. En lugar de una puntuación puntual, el sistema entrega un intervalo de confianza: un rango dentro del cual es altamente probable que se encuentre la evaluación correcta. Este enfoque no solo mejora la fiabilidad de los juicios automatizados, sino que también transforma radicalmente la forma en que entendemos la evaluación por inteligencia artificial.
La clave de este avance reside en una técnica estadística llamada predicción conforme (conformal prediction). A diferencia de otros métodos que intentan que el modelo “adivine” su propia confianza (algo en lo que suelen fracasar por sobreconfianza o incoherencia), la predicción conforme opera de forma externa al modelo. No requiere reentrenarlo ni modificar su arquitectura. Simplemente observa cómo se ha comportado el modelo en ejemplos previos y, a partir de ahí, construye garantías estadísticas sobre su desempeño futuro. Es como si, tras ver a un meteorólogo acertar (o fallar) en sus pronósticos durante un año, pudiéramos calcular con precisión cuán probable es que su próxima predicción sea correcta.
Este enfoque es especialmente poderoso porque es agnoóstico del modelo: funciona con GPT, con Qwen, con Llama o con cualquier otro LLM, siempre que pueda generar puntuaciones. Además, es post hoc, lo que significa que se aplica después de que el modelo ya ha hecho su trabajo, sin interferir en su lógica interna. Y, lo más importante, ofrece garantías de cobertura: si se pide un intervalo con un 90 % de confianza, entonces, en promedio, el 90 % de las veces ese intervalo contendrá la puntuación correcta.
El estudio no se limita a proponer esta idea en abstracto. Sus autores la ponen a prueba en múltiples escenarios reales: resúmenes de noticias, diálogos, razonamiento lógico, incluso tareas multimodales que combinan texto e imagen. Evalúan nueve métodos distintos de predicción conforme, comparan tres modelos de lenguaje diferentes y analizan cómo varía la calidad de los intervalos según el tipo de tarea. Pero su contribución más innovadora es un ajuste sutil pero crucial: dado que las evaluaciones humanas suelen ser discretas (por ejemplo, puntuaciones enteras del 1 al 5), los intervalos continuos generados por métodos estándar pueden resultar confusos o ineficientes. Para resolverlo, diseñan un ajuste de límites que alinea los extremos del intervalo con las puntuaciones posibles, mejorando la cobertura sin sacrificar la precisión.
Más allá de los intervalos, el trabajo explora cómo utilizarlos. ¿Qué hacer con un rango de puntuaciones en lugar de una sola cifra? Los investigadores proponen usar el punto medio del intervalo como una estimación más precisa y menos sesgada que la puntuación bruta del modelo. Sus experimentos demuestran que este punto medio se acerca más al juicio humano, con errores significativamente menores. Incluso exploran si es útil “re-preguntarle” al modelo mostrándole su propio intervalo de incertidumbre, aunque descubren que los LLMs tienden a aferrarse a su juicio inicial, incluso cuando este cae fuera del rango sugerido.
En conjunto, este trabajo representa un paso decisivo hacia una inteligencia artificial más humilde, transparente y útil. No se trata de construir modelos infalibles —una quimera—, sino de dotarlos de la capacidad de reconocer sus propios límites. En un mundo donde los LLMs están empezando a influir en decisiones críticas, esa capacidad no es un lujo técnico; es una necesidad ética.
De la puntuación puntual al intervalo de confianza
Durante años, la evaluación automática de textos generados por inteligencia artificial ha sido un campo plagado de atajos y compromisos. Métricas clásicas como BLEU o ROUGE comparan palabras o frases entre el texto generado y una referencia humana, pero a menudo fallan al capturar la fluidez, la coherencia o la relevancia semántica. Los modelos de lenguaje grandes prometieron una solución más sofisticada: en lugar de contar coincidencias, podrían entender el contenido y emitir juicios cualitativos, casi como un ser humano.
Así nació el paradigma de “LLM-as-a-judge”. En su forma más simple, se le da al modelo una instrucción detallada (por ejemplo, “Evalúa la coherencia del siguiente resumen en una escala del 1 al 5”) y se le pide que genere una puntuación. Los resultados han sido impresionantes: en muchos benchmarks, las evaluaciones de los LLMs coinciden fuertemente con las de los anotadores humanos. Esto ha llevado a su adopción generalizada en la investigación y la industria, ya que ofrecen una alternativa barata y rápida a la anotación manual.
Sin embargo, esta aparente solidez esconde una fragilidad fundamental. Un LLM, por su naturaleza, es un sistema estocástico: su salida puede variar ligeramente incluso con la misma entrada, dependiendo de factores como la temperatura de muestreo o el ruido interno. Además, su juicio puede estar sesgado por la forma en que fue entrenado, por los ejemplos que vio o por la redacción de la instrucción. Peor aún, los LLMs son notorios por su sobreconfianza: tienden a presentar respuestas erróneas con la misma seguridad que las correctas.
El problema no es que el modelo se equivoque ocasionalmente, eso es inevitable, sino que no ofrece ninguna pista sobre cuándo lo hace. Para un usuario final, una puntuación de “3” es indistinguible de una puntuación de “3 con alta certeza” o “3, pero podría ser 1 o 5”. Esta falta de granularidad en la incertidumbre limita gravemente la utilidad del juicio en contextos donde la precisión es crítica.
Aquí es donde entra en juego la predicción conforme. En lugar de pedir al modelo que calibre su propia confianza, una tarea en la que ha demostrado ser poco fiable, este enfoque construye una “correa de seguridad” estadística desde fuera. El proceso es elegante en su simplicidad:
Primero, se reserva un conjunto de datos de calibración: ejemplos similares a los que se evaluarán, pero cuya puntuación “verdadera” (por ejemplo, el promedio de varios anotadores humanos) ya se conoce. Luego, se ejecuta el LLM en este conjunto y se registran sus puntuaciones y, crucialmente, sus logits, los valores internos que el modelo asigna a cada posible token antes de convertirlos en probabilidades. A partir de estos logits y las puntuaciones reales, se calcula una puntuación de no conformidad para cada ejemplo: una medida de cuán “inusual” fue la predicción del modelo en comparación con la verdad. Por ejemplo, si el modelo predijo un 4 y la verdad era un 2, la no conformidad será alta; si predijo un 3 y la verdad era un 3.1, será baja.
Finalmente, para un nuevo ejemplo a evaluar, se calcula su puntuación de no conformidad hipotética para cada valor posible en la escala. El intervalo de predicción se define como el conjunto de valores cuya no conformidad es menor o igual a un umbral estadístico derivado del conjunto de calibración. Este umbral se elige de modo que, con una probabilidad preespecificada (por ejemplo, el 90 %), la puntuación verdadera caerá dentro del intervalo.
El resultado es transformador: en lugar de una cifra solitaria, el usuario recibe un mensaje como: “La puntuación está entre 2 y 4, con un 90 % de confianza”. Esto no solo comunica la evaluación, sino también su fiabilidad. Un intervalo estrecho (por ejemplo, [3.8, 4.2]) sugiere alta certeza; uno amplio ([1, 5]) es una bandera roja que indica que el modelo está muy inseguro y que la decisión merece una revisión humana.
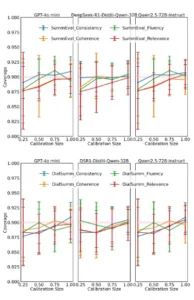
El reto de las escalas discretas y la solución del ajuste de límites
La predicción conforme, en su formulación clásica, está diseñada para tareas de regresión, donde la variable objetivo es continua. Sin embargo, la evaluación humana de textos rara vez funciona así. Las puntuaciones suelen ser discretas y ordinales: un 1, 2, 3, 4 o 5 en una escala Likert, donde el orden importa (5 es mejor que 4) pero la distancia entre los puntos no necesariamente es uniforme.
Aplicar directamente los métodos de predicción conforme a este contexto genera un problema de interpretación. Imaginemos que el método produce un intervalo continuo como [2.2, 3.9]. ¿Qué significa esto en la práctica? ¿Debemos redondear a [2, 4]? ¿O truncar a [3, 3]? Cada opción tiene consecuencias: redondear podría ampliar innecesariamente el intervalo y perder precisión, mientras que truncar podría excluir puntuaciones válidas y violar la garantía de cobertura.
Los autores del estudio identifican este desafío y proponen una solución ingeniosa: un ajuste de límites (boundary adjustment) que transforma el intervalo continuo en uno discreto de forma teóricamente fundamentada. La idea es simple pero poderosa: en lugar de redondear arbitrariamente, se redefine la función de no conformidad para que, al construir el intervalo, sus extremos se “ajusten” a las puntuaciones enteras más cercanas.
Este ajuste no es un truco ad hoc; viene acompañado de una demostración matemática. El Teorema 1 del artículo prueba que este procedimiento no reduce la cobertura del intervalo. De hecho, en muchos casos la aumenta, porque al expandir ligeramente los límites para incluir puntuaciones enteras adyacentes, se capturan casos que antes caían justo fuera del intervalo continuo. Por ejemplo, si la puntuación verdadera es un 2 y el intervalo continuo es [2.1, 3.9], el ajuste lo expandiría a [2, 3], incluyendo así la verdad y mejorando la cobertura. Los experimentos del estudio confirman la eficacia de esta estrategia. En todos los conjuntos de datos y con todos los modelos probados, el ajuste de límites mejora consistentemente la tasa de cobertura, a menudo llevándola al nivel deseado del 90 %, sin aumentar significativamente la anchura del intervalo. En algunos casos, incluso la reduce, al eliminar “ruido” en los extremos continuos que no corresponden a puntuaciones reales.
Este avance es crucial porque hace que la predicción conforme sea práctica y comprensible para los usuarios finales. Un intervalo discreto como [2, 4] es inmediatamente interpretable: significa que, según el modelo y su historial de errores, la puntuación correcta es muy probablemente un 2, un 3 o un 4. Esta claridad es esencial para que los intervalos de confianza se integren en flujos de trabajo reales, desde la revisión de ensayos automatizados hasta la evaluación de diagnósticos médicos generados por IA.
Más allá del intervalo: el punto medio como puntuación calibrada
Una vez que se dispone de un intervalo de confianza, surge una pregunta natural: ¿cómo se usa esa información para tomar una decisión? En muchos casos, el usuario aún necesita una puntuación única para, por ejemplo, ordenar varios textos o decidir si un resumen es lo suficientemente bueno como para ser publicado.
Una opción ingenua sería usar la puntuación bruta que el LLM emitió originalmente. Otra sería usar un promedio ponderado de las probabilidades de cada puntuación, una técnica común en el framework G-Eval. Pero el estudio propone una tercera vía, más robusta: usar el punto medio del intervalo de predicción.
La lógica es intuitiva. Si sabemos que la puntuación verdadera está, con alta probabilidad, dentro de un rango, entonces el centro de ese rango es una estimación más informada que cualquier puntuación aislada. Es como si, en lugar de confiar en una sola medición de un instrumento ruidoso, se tomara el promedio de todas las mediciones posibles que son consistentes con la incertidumbre del instrumento.
Los resultados experimentales son contundentes. El punto medio del intervalo (especialmente cuando se calcula con el método R2CCP, identificado como el más eficiente en el estudio) supera consistentemente a las puntuaciones brutas y a los promedios ponderados en términos de error absoluto medio (MAE) y error cuadrático medio (MSE). En algunos casos, la reducción del error es dramática: en la dimensión de fluidez del conjunto SummEval, el MSE se reduce en un 88.7 % al usar el punto medio en lugar de la puntuación bruta del modelo.
Esto tiene implicaciones profundas. Significa que el intervalo de confianza no es solo una medida de incertidumbre pasiva, sino una herramienta activa para mejorar la calidad de la evaluación. El punto medio actúa como una puntuación calibrada, que corrige sistemáticamente los sesgos y errores del modelo original. Es una forma de extraer más valor de la misma evaluación, simplemente reconociendo y cuantificando su incertidumbre.
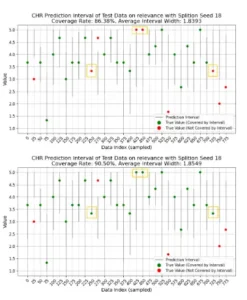
Factores que moldean la calidad de la incertidumbre
El estudio no se limita a proponer un método; también realiza un análisis exhaustivo de los factores que influyen en la calidad de los intervalos de predicción. Sus hallazgos ofrecen una hoja de ruta práctica para quienes deseen implementar este enfoque.
En primer lugar, la elección del modelo de lenguaje importa. Los autores comparan tres LLMs: GPT-4o mini, DeepSeek-R1-Distill-Qwen-32B y Qwen2.5-72B-Instruct. Descubren que, si bien todos pueden beneficiarse de la predicción conforme, hay diferencias sutiles. Qwen2.5-72B-Instruct tiende a producir los intervalos más estrechos, lo que sugiere una mayor precisión en sus juicios. En cambio, DeepSeek-R1-Distill-Qwen-32B ofrece la cobertura más consistente, lo que lo hace ideal para aplicaciones de alto riesgo donde es crucial no subestimar la incertidumbre.
En segundo lugar, el tamaño del conjunto de calibración es un factor crítico. La predicción conforme depende de tener suficientes ejemplos para estimar de forma fiable la distribución de la no conformidad. El estudio demuestra que, a medida que se reduce el tamaño del conjunto de calibración, la cobertura se vuelve más inestable y la anchura de los intervalos más variable. Esto implica un trade-off práctico: para obtener garantías sólidas, se necesita una inversión inicial en datos anotados por humanos. No se puede construir una “correa de seguridad” estadística sin un historial de errores sobre el que basarla.
En tercer lugar, la naturaleza de la tarea de evaluación influye en la dificultad. El estudio compara tareas de resumen de texto con tareas de razonamiento lógico. Encontró que, en general, los LLMs son más confiables al evaluar resúmenes, donde los intervalos son más estrechos y la cobertura más fácil de lograr. En cambio, en tareas de razonamiento, la incertidumbre es intrínsecamente mayor, lo que se refleja en intervalos más amplios. Esto sugiere que la predicción conforme no solo mide la incertidumbre del modelo, sino también la complejidad inherente de la tarea.
Finalmente, el método de predicción conforme elegido tiene un impacto significativo. De los nueve métodos evaluados, R2CCP emerge como el más equilibrado, ofreciendo una excelente relación entre cobertura y eficiencia (anchura del intervalo). Otros métodos, como LVD, pueden ser útiles si la prioridad absoluta es la cobertura, mientras que Boosted LCP es una opción sólida si se dispone de recursos computacionales para el proceso de refuerzo.
Los límites de la autorreflexión: ¿puede un LLM aprender de su propia incertidumbre?
Una de las preguntas más fascinantes que plantea el estudio es si la incertidumbre cuantificada puede ser utilizada para mejorar el propio juicio del modelo. En otras palabras, si se le muestra al LLM su intervalo de confianza del 90 %, ¿será capaz de reflexionar sobre él y ajustar su puntuación para acercarla a la verdad?
Los autores diseñaron un experimento ingenioso para probar esta hipótesis. Primero, obtuvieron una puntuación inicial del modelo. Luego, le proporcionaron su intervalo de confianza y le pidieron que reconsiderara su juicio, explicando su razonamiento paso a paso.
Los resultados fueron reveladores, pero no en el sentido esperado. En la mayoría de los casos, el modelo no cambió su puntuación, incluso cuando esta caía fuera del intervalo sugerido. Las explicaciones posteriores mostraban que el LLM entendía el concepto de intervalo y reconocía que su puntuación inicial estaba en el límite, pero se aferraba a su juicio original con una confianza inquebrantable. Era como si dijera: “Sé que podría estar equivocado, pero sigo pensando que tengo razón”.
Este comportamiento pone de manifiesto una limitación fundamental de los LLMs actuales: carecen de un mecanismo genuino de autorreflexión crítica. Pueden simular el proceso de reconsideración, pero no poseen la humildad epistémica para cuestionar seriamente sus propias conclusiones a la luz de nueva evidencia. Su “razonamiento” sigue estando anclado en su primera impresión.
Sin embargo, hubo una excepción interesante. Cuando se les permitió a los modelos generar puntuaciones no enteras (por ejemplo, 4.33 en lugar de 4), algunos sí ajustaron su juicio hacia el límite inferior del intervalo. Esto sugiere que la rigidez de las escalas discretas también juega un papel: si el modelo siente que la única alternativa a un 4 es un 5 (un salto demasiado grande), prefiere quedarse con el 4, aunque el intervalo sugiera que la verdad está en algún punto intermedio.
Este hallazgo tiene implicaciones importantes para el diseño de interfaces humano-IA. En lugar de esperar que los modelos se autocorrijan, es más eficaz que el sistema presente directamente la información de incertidumbre al usuario humano, quien puede entonces tomar una decisión informada. La IA no tiene por qué ser el juez final; puede ser un asesor que dice: “Esto es lo que pienso, y esto es cuán seguro estoy de ello”.
Hacia una inteligencia artificial más humilde y útil
El trabajo presentado en Analyzing Uncertainty of LLM-as-a-Judge es mucho más que un avance técnico en un nicho de la evaluación de IA. Es una declaración de principios sobre cómo debería funcionar la tecnología en un mundo complejo e incierto.
En la carrera por construir modelos cada vez más grandes y poderosos, se ha perdido de vista una virtud humana fundamental: la humildad intelectual. Saber cuándo no se sabe algo es, en muchos sentidos, más valioso que saberlo todo. La predicción conforme, al dotar a los LLMs de una forma rigurosa de expresar su incertidumbre, les inyecta un poco de esa humildad.
Esta capacidad es esencial para la confianza responsable. No se trata de confiar ciegamente en la IA, sino de entender sus límites y actuar en consecuencia. Un intervalo de confianza amplio no es un fallo del sistema; es una característica de diseño que previene errores costosos. En medicina, podría evitar un diagnóstico erróneo. En justicia, podría impedir que un algoritmo influya indebidamente en una sentencia. En educación, podría señalar que un ensayo merece una segunda mirada humana.
Además, este enfoque democratiza la evaluación de IA. Al ser agnóstico del modelo y post hoc, puede aplicarse a cualquier sistema, incluso a aquellos cuyo código o arquitectura son propietarios y opacos. Esto es crucial en un ecosistema donde los modelos comerciales dominan el panorama, pero su comportamiento interno es un misterio para la mayoría de los usuarios.
En última instancia, el verdadero logro de este estudio es haber cambiado la pregunta. Ya no se trata de “¿qué puntuación dio el modelo?”, sino de “¿qué tan seguro está el modelo de su puntuación?”. Esta sutil pero profunda reorientación es la que separa a una IA que pretende ser infalible de una IA que aspira a ser una socio fiable. Y en un futuro donde la inteligencia artificial estará cada vez más entrelazada con nuestras vidas, ese es el único tipo de socio que podemos permitirnos.
Referencias
Sheng, H., Liu, X., He, H., Zhao, J., & Kang, J. (2025). Analyzing Uncertainty of LLM-as-a-Judge: Interval Evaluations with Conformal Prediction. arXiv preprint arXiv:2509.18658.



