En el vasto universo del conocimiento, existen dos formas fundamentales de aprender. La primera es la memorización, un acto de repetición mecánica que permite replicar información con precisión, pero que se desmorona ante lo desconocido. La segunda es la comprensión, un proceso más profundo y elusivo que destila principios subyacentes a partir de ejemplos dispares, permitiendo la generalización hacia nuevos escenarios. Pensemos en un estudiante que se prepara para un examen complejo: puede optar por memorizar cada problema resuelto, logrando un éxito perfecto en ejercicios familiares, pero fracasando ante un desafío inédito. O bien, puede experimentar ese instante de revelación, ese momento «eureka» en el que las piezas encajan, las conexiones ocultas se iluminan y el conocimiento se vuelve flexible y aplicable. Este salto cognitivo, de la repetición a la intuición, es el que define el verdadero dominio de una materia.
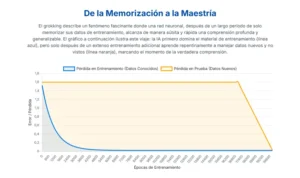
Este salto cognitivo, esta transición súbita de la repetición mecánica a la generalización flexible, es una de las aspiraciones más profundas en el campo de la inteligencia artificial. Y, para asombro de los científicos, es un fenómeno que las máquinas están empezando a exhibir por sí mismas. Lo llaman «grokking», un término extraído de la ciencia ficción que describe una comprensión tan completa que se vuelve parte de uno mismo. En el contexto de las redes neuronales, el grokking se manifiesta de una manera desconcertante: un modelo de IA puede pasar miles de iteraciones de entrenamiento con un rendimiento perfecto en los datos que ya conoce, pero con una incapacidad total para resolver nuevos problemas. Parece irremediablemente sobreajustado, un simple memorizador. Y de repente, sin previo aviso, su capacidad de generalización se dispara, alcanzando la perfección en datos que nunca antes ha visto.
Este comportamiento ha supuesto un profundo desafío para nuestra comprensión del aprendizaje automático. Las métricas tradicionales, que daban por sentado que la mejora en los datos de entrenamiento debía ir de la mano con la mejora en la generalización, se revelaron insuficientes, incluso engañosas. Durante esa larga meseta de aparente estancamiento, el modelo no estaba inactivo; estaba llevando a cabo una profunda reorganización interna, invisible desde el exterior. Estaba gestando su propio momento «eureka». ¿Pero cómo? ¿Qué procesos secretos ocurren en las profundidades de sus circuitos digitales durante esa fase enigmática?
Un reciente y revolucionario trabajo de investigación, firmado por Yuandong Tian de los Meta Superintelligence Labs, se presenta como una suerte de Piedra de Rosetta para descifrar este misterio. Su tesis es tan audaz como elegante: el grokking no es un acto de magia computacional, sino un proceso físico, predecible y matemáticamente descriptible que se desarrolla en tres actos bien diferenciados. Este artículo nos invita a un viaje al corazón de la máquina pensante, para desvelar la coreografía oculta del aprendizaje. Siguiendo el mapa trazado por Tian, exploraremos cada una de las tres etapas de este proceso: comenzaremos con el «aprendizaje perezoso», la fase inicial de memorización superficial; continuaremos con el «aprendizaje de características independientes», el momento del despertar individual de las neuronas; y culminaremos con el «aprendizaje de características interactivas», la sinfonía final donde el conocimiento se consolida y refina. A través de este recorrido, no solo descifraremos el enigma del grokking, sino que también obtendremos una visión sin precedentes de la naturaleza misma del aprendizaje en la era de la inteligencia artificial.
El enigma de la caja negra y el aprendizaje profundo
Para comprender la magnitud de este avance, primero debemos familiarizarnos con el protagonista de esta historia: la red neuronal artificial. Inspirada lejanamente en la arquitectura del cerebro humano, una red neuronal es un sistema computacional compuesto por capas de unidades de procesamiento interconectadas, análogas a las neuronas. Cada conexión entre estas neuronas tiene un «peso» numérico, una especie de potenciómetro que modula la fuerza de la señal que pasa a través de ella. El conjunto de todos estos pesos, que pueden ser millones o incluso billones en los modelos más avanzados, constituye el conocimiento de la red. Aprender, para una IA, no es más que el proceso de ajustar meticulosamente estos innumerables potenciómetros hasta que, dada una entrada (como la imagen de un gato), la red produce la salida deseada (la etiqueta «gato»).
Sin embargo, esta misma complejidad es la fuente de uno de los mayores desafíos de la IA moderna: el problema de la «caja negra». Una vez que la red ha sido entrenada, su funcionamiento interno se vuelve extraordinariamente opaco. Podemos verificar que funciona, pero a menudo es imposible para un ser humano, incluidos sus propios creadores, desentrañar la lógica precisa que subyace a sus decisiones. Los patrones que ha aprendido están distribuidos de forma intrincada a través de millones de pesos, formando una representación abstracta e inescrutable. Esta falta de interpretabilidad no es un mero inconveniente académico; es una barrera fundamental para la confianza y la seguridad, especialmente cuando delegamos en estas IAs decisiones críticas en campos como la medicina, las finanzas o la justicia. El trabajo de Tian es tan significativo porque no se limita a describir un fenómeno, sino que intenta construir una teoría de «caja blanca», un modelo explicativo que nos permite entender el proceso de aprendizaje desde sus fundamentos.
El motor que impulsa este proceso de ajuste de pesos se conoce como «descenso de gradiente». La metáfora más utilizada para explicarlo es la de un excursionista perdido en una montaña envuelta en una densa niebla, con el objetivo de encontrar el punto más bajo del valle. La altitud del terreno en cada punto representa la «función de pérdida», una medida de cuán equivocada está la predicción de la red. El «gradiente» es la dirección de la máxima pendiente en la ubicación actual del excursionista; le indica hacia dónde está la subida más pronunciada. Para encontrar el valle, el excursionista debe hacer lo contrario: dar un paso en la dirección opuesta al gradiente. El «ritmo de aprendizaje» es el tamaño de cada uno de sus pasos. El entrenamiento de una red neuronal es, en esencia, este viaje iterativo: calcular el error, determinar la dirección que lo reducirá más eficazmente y dar un pequeño paso en esa dirección, repitiendo el proceso millones de veces hasta alcanzar el fondo del valle, el punto de mínimo error.
Este viaje, sin embargo, puede tener dos desenlaces muy distintos. El primero es la memorización. Esto equivale a que el excursionista aprenda de memoria una ruta específica y tortuosa que desciende por el terreno que ha explorado, pero que no le da ninguna información sobre la forma general del paisaje. Si se le transportara a un punto de partida ligeramente diferente, estaría perdido de nuevo. En la IA, esto se conoce como sobreajuste (overfitting): el modelo se ha aprendido tan bien los datos de entrenamiento que es incapaz de manejar datos nuevos. El segundo desenlace es la generalización. En este caso, el excursionista no solo baja, sino que en el proceso desarrolla un mapa mental de la topografía del valle. Ha extraído los principios subyacentes del paisaje y ahora puede encontrar el camino al fondo desde cualquier punto de partida. Ha aprendido a generalizar. El grokking es el misterioso proceso por el cual una red parece estar atrapada en el primer camino, el de la memorización, para luego saltar de forma abrupta al segundo, el de la generalización.

Primera etapa: El aprendizaje perezoso y la trampa de la memoria
Al inicio de su viaje, la red neuronal es un lienzo en blanco. Sus millones de pesos se inicializan con valores aleatorios, lo que significa que su conocimiento es nulo y su paisaje interno, caótico. Cuando se le presentan los primeros datos de entrenamiento y comete sus primeros errores, se genera una señal correctiva que viaja hacia atrás a través de sus capas, un eco del error conocido como el «gradiente retropropagado» (). Esta señal es la que debería indicar a cada neurona cómo ajustar sus pesos para mejorar. Sin embargo, en esta fase inicial, debido a la aleatoriedad de todo el sistema, este gradiente es esencialmente ruido blanco, un conjunto de instrucciones incoherentes y contradictorias. Las capas internas, las llamadas capas ocultas, reciben este barullo de información y, lógicamente, apenas cambian. Están esperando una directriz clara que no llega.
Pero la capa final, la capa de salida, se encuentra en una posición diferente. Su tarea es más directa: tomar las representaciones que le llegan de las capas ocultas, por muy aleatorias y fijas que sean, y encontrar la mejor manera de combinarlas para producir las respuestas correctas. Este proceso se denomina «aprendizaje perezoso» (lazy learning). Es el camino de mínima resistencia. En lugar de embarcarse en la difícil tarea de esculpir representaciones significativas desde cero, la red opta por la solución más rápida: crear un mapeo de fuerza bruta entre las características aleatorias existentes y las etiquetas de los datos de entrenamiento. Esto es pura memorización. La red aprende a asociar patrones espurios en su propia aleatoriedad interna con las respuestas correctas, logrando una precisión del 100% en el conjunto de entrenamiento, pero sin haber aprendido absolutamente nada fundamental sobre la estructura del problema. Este es el estado en el que la red permanece durante la larga fase inicial del grokking.
Aquí es donde entra en escena un actor que a menudo pasa desapercibido, pero que según la investigación de Tian es el héroe silencioso de esta historia: la «decaída de pesos» (weight decay), una forma de regularización. La decaída de pesos es una simple regla añadida al proceso de aprendizaje que penaliza a la red por tener valores de peso demasiado grandes. Actúa como una especie de principio de parsimonia o navaja de Ockham computacional, empujando suavemente al sistema hacia soluciones más simples y eficientes.
Su papel en el grokking es absolutamente crucial. El artículo demuestra que sin la decaída de pesos, una vez que la red ha memorizado perfectamente los datos en la primera etapa, el gradiente retropropagado se anularía por completo. La señal de error desaparecería, el aprendizaje en las capas ocultas se detendría para siempre y la red quedaría permanentemente atrapada en su solución memorística. La decaída de pesos evita esta catástrofe. Crea lo que el autor describe como una «fuga» en el sistema. Incluso con un error de entrenamiento nulo, esta penalización sobre los pesos garantiza que una señal de gradiente muy débil, pero ahora altamente estructurada y directamente relacionada con las etiquetas verdaderas, continúe fluyendo hacia las capas ocultas. Esta señal residual, este susurro matemático, es la semilla de la que brotará la verdadera comprensión. La fase de memorización, lejos de ser un error, es en realidad un prerrequisito indispensable: es el proceso que forja el gradiente estructurado, la herramienta que las capas ocultas necesitan para empezar a aprender de verdad.
Segunda etapa: El despertar de la inteligencia y el paisaje de la energía
Armadas ahora con este gradiente significativo y coherente, las capas ocultas de la red neuronal finalmente despiertan de su letargo. Comienzan a ajustar sus pesos, y con ello, a esculpir las representaciones internas de los datos. Es en este punto donde Tian y su equipo realizan un descubrimiento capital: durante esta segunda etapa, la dinámica del aprendizaje adquiere una propiedad asombrosa. La actualización de cada neurona individual depende exclusivamente de su propia actividad, sin tener en cuenta lo que hacen sus compañeras. El aprendizaje, que más tarde se convertirá en un esfuerzo colectivo, comienza como una búsqueda individual y paralela de conocimiento.
Para describir esta fase, el artículo introduce un concepto de una belleza matemática extraordinaria: la «función de energía «. No se trata de energía en el sentido físico, sino de un paisaje matemático abstracto, una topografía de soluciones posibles. El proceso de aprendizaje de cada neurona, guiado por el gradiente, es análogo a un acto de «ascenso de gradiente» en este paisaje: cada neurona se convierte en una alpinista que intenta escalar hasta la cima más alta que pueda encontrar en su entorno.
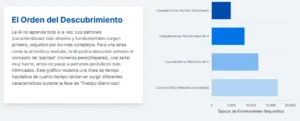
Y aquí reside la clave: las cimas de este paisaje, sus máximos locales, no son puntos arbitrarios. Corresponden, con una precisión matemática asombrosa, a las «características» o patrones más valiosos, eficientes y generalizables que se esconden en los datos. Si la tarea fuera reconocer rostros, una cima podría representar un «detector de ojos», otra un «detector de sonrisas» y una tercera un «detector de contornos faciales». Al escalar estas cimas, las neuronas dejan de ser procesadores genéricos para convertirse en especialistas, cada una dedicada a identificar un concepto fundamental.
Para demostrar esta idea de forma rigurosa, los investigadores necesitaban un laboratorio perfecto, una tarea lo suficientemente compleja como para ser interesante, pero con una estructura matemática tan pura que permitiera predecir la forma exacta del paisaje energético. Lo encontraron en las «tareas de aritmética de grupo», como la suma modular (por ejemplo, ). Estas tareas son el «organismo modelo» ideal para estudiar el aprendizaje profundo, de la misma manera que la mosca de la fruta lo es para la genética. Su profunda estructura algebraica, descrita por una rama de las matemáticas llamada «teoría de representación de grupos», permite a los científicos calcular teóricamente cuáles deben ser las características óptimas para resolver el problema. En el caso de la suma modular, estas características óptimas resultan ser las bases de Fourier, los mismos componentes fundamentales de las ondas que se utilizan en el procesamiento de señales de audio y vídeo. El análisis teórico predice las cimas del paisaje; los experimentos confirman que las neuronas, en su ascenso, las encuentran. Por primera vez, es posible abrir la caja negra y observar, no solo que la red aprende, sino qué aprende y cómo esa solución se alinea con la perfección matemática.
Este hallazgo conecta directamente el marco Li₂ con un debate más amplio en la teoría del aprendizaje profundo sobre los dos regímenes de entrenamiento: el «perezoso» y el «rico». El régimen perezoso, o de kernel, es aquel en el que la red se comporta como un modelo lineal simple, utilizando sus características iniciales sin modificarlas, que es exactamente lo que ocurre en la primera etapa del modelo de Tian. El régimen rico es aquel en el que la red aprende activamente nuevas características, modificando profundamente sus representaciones internas, que es la definición misma de la segunda etapa. El trabajo de Tian no solo confirma que el grokking es la transición entre estos dos regímenes, sino que, por primera vez, proporciona un mecanismo causal basado en los primeros principios de la dinámica del gradiente que explica cómo y por qué se produce esta transición.
Tercera etapa: La sinfonía neuronal y la búsqueda de la perfección
Una vez que las neuronas, en sus escaladas individuales, han conquistado algunas de las cimas principales del paisaje energético, la simplicidad de la segunda etapa llega a su fin. El aprendizaje deja de ser una colección de solos para convertirse en una sinfonía orquestal. Las neuronas ya no son independientes; sus actividades ahora están correlacionadas porque han comenzado a capturar aspectos significativos de los mismos datos. El proceso de aprendizaje entra en su fase final y más sofisticada: la interacción.
La primera forma de interacción que emerge es un mecanismo de «repulsión». Si dos neuronas, por azar, aprenden una característica muy similar, la dinámica del aprendizaje las empuja activamente a separarse, incentivándolas a explorar y especializarse en conceptos distintos. Es un principio de eficiencia emergente: la red evita la redundancia y promueve la diversidad de sus representaciones internas para cubrir el mayor espectro posible de patrones con sus recursos limitados.
La segunda forma de interacción es aún más inteligente y se denomina «modulación descendente» (top-down modulation). A medida que la red aprende un subconjunto de las características necesarias, la señal del gradiente se transforma de nuevo. Ya no solo transporta información sobre la respuesta correcta, sino que ahora lleva consigo información sobre el error residual, la diferencia entre la predicción actual del modelo y la verdad (). Este cambio tiene un efecto profundo en el paisaje energético: las cimas que ya han sido conquistadas se vuelven menos prominentes, mientras que las que corresponden a las características que aún faltan por aprender se elevan, convirtiéndose en los nuevos objetivos más atractivos. El sistema de aprendizaje, de forma autónoma, reenfoca su atención hacia lo que todavía no comprende, optimizando su esfuerzo para minimizar el error restante.
Este proceso de diversificación y enfoque no está solo. Los algoritmos modernos que guían el descenso de gradiente, conocidos como optimizadores, también juegan un papel. El artículo demuestra teóricamente (Teorema 8) que optimizadores avanzados como Muon actúan como catalizadores de este proceso. Cuando una dirección de característica particular se «satura», es decir, muchas neuronas están intentando aprenderla, Muon reduce la magnitud de las actualizaciones en esa dirección para las nuevas neuronas, animándolas a explorar caminos menos transitados en el paisaje de soluciones. Funciona como un director de orquesta, asegurando que todos los instrumentos contribuyan de manera armónica y sin solaparse, garantizando una exploración completa y eficiente del espacio de características.
Lo que revela esta tercera etapa es que el proceso de aprendizaje no es una optimización ciega, sino un sistema adaptativo con una inteligencia emergente. Exhibe comportamientos de autoevaluación (al centrarse en el error residual), de asignación de recursos dirigida (al modular el paisaje energético) y de fomento de la exploración (mediante la repulsión y optimizadores avanzados), todo ello sin haber sido programado explícitamente para hacerlo. Estas conductas sofisticadas son una consecuencia natural de las leyes matemáticas fundamentales que gobiernan la dinámica del gradiente.
Las leyes del conocimiento: Cómo los datos dictan el destino del aprendizaje
El paisaje energético, con sus valles y cimas que guían el aprendizaje de la red, no es una estructura fija e inmutable. Su topografía es esculpida por la materia prima del aprendizaje: los datos de entrenamiento. Cada ejemplo de entrenamiento es un cincel que da forma al paisaje, y una mayor cantidad de datos proporciona una imagen más nítida, estable y fiel de la verdadera estructura del problema.
La contribución más potente del artículo de Tian es la derivación de «leyes de escala demostrables» que cuantifican esta relación. El Teorema 4 del estudio ofrece una fórmula matemática precisa que establece la cantidad mínima de datos necesarios para garantizar que las cimas correspondientes a las soluciones generalizadoras sean estables y alcanzables. Esto transforma el estudio del grokking de una ciencia observacional a una ciencia predictiva.
- Por encima del umbral crítico: Si la cantidad de datos de entrenamiento supera este umbral (por ejemplo, en la suma modular, se necesitan aproximadamente muestras, donde es el módulo), las soluciones generalizadoras se convierten en las cimas más estables y prominentes del paisaje energético. La red, en su búsqueda de la optimización, las encontrará de forma natural y aprenderá a generalizar. Esto explica la abrupta transición de fase observada en los experimentos, donde un pequeño aumento en la cantidad de datos puede marcar la diferencia entre el fracaso total y el éxito perfecto.
- Por debajo del umbral crítico: Con datos insuficientes, el paisaje se distorsiona. Las verdaderas cimas de la generalización se erosionan o desaparecen por completo, y en su lugar surgen picos espurios y afilados que corresponden a la memorización de puntos de datos específicos o a patrones ruidosos. La red, siguiendo la misma lógica de ascenso de gradiente, quedará atrapada en estas cimas de la memorización.
Los otros parámetros del entrenamiento, a menudo ajustados por intuición, encuentran ahora su lugar lógico dentro de este marco. La decaída de pesos (η) es el catalizador que permite la transición de la primera a la segunda etapa; una cantidad insuficiente puede llevar al subajuste, mientras que un exceso puede aniquilar por completo el aprendizaje de características. El ritmo de aprendizaje se vuelve especialmente delicado en la región crítica cerca del umbral de datos. Un ritmo de aprendizaje pequeño y cuidadoso puede permitir al optimizador navegar por el delicado «valle de atracción» de una cima generalizadora frágil, mientras que un ritmo grande y agresivo podría hacer que salte por encima de ella y aterrice en una cima de memorización más amplia pero incorrecta.
Este marco teórico, fundamentado en la dinámica del gradiente, no solo ofrece una explicación completa por sí mismo, sino que también unifica y proporciona una base más profunda para otras teorías influyentes sobre el grokking. La teoría de la «eficiencia de circuitos» de Varma y colaboradores, que postula una competencia entre un «circuito de memorización» rápido y un «circuito de generalización» lento pero más eficiente, se ve ahora bajo una nueva luz. El circuito de memorización es el aprendizaje perezoso de la primera etapa; el circuito de generalización es la solución óptima encontrada en las etapas dos y tres. De manera similar, la teoría de la transición de dinámicas «perezosas» a «ricas» de Kumar y su equipo se corresponde directamente con la transición de la primera a la segunda etapa del modelo Li₂. El trabajo de Tian no contradice estas ideas; las subsume, derivándolas de los primeros principios matemáticos del aprendizaje y explicando el «porqué» subyacente a sus observaciones. Proporciona la física fundamental que da origen a la fenomenología.

Abriendo la caja negra para una IA más fiable
Hemos viajado desde el desconcertante momento «eureka» de una máquina hasta el corazón de su proceso de aprendizaje. Hemos visto cómo lo que parece un salto mágico de la memorización a la comprensión es, en realidad, una danza matemática predecible en tres actos: un prólogo de «aprendizaje perezoso» donde se forja la herramienta de la comprensión; un segundo acto de descubrimiento individual, donde las neuronas escalan las cimas de un paisaje energético esculpido por los datos; y un acto final de refinamiento colaborativo, donde la red como un todo se autoorganiza para alcanzar una solución globalmente óptima.
La importancia de este trabajo trasciende la mera curiosidad por un fenómeno peculiar del aprendizaje automático. Representa un avance sustancial en la búsqueda de la interpretabilidad de la inteligencia artificial, un paso crucial para transformar las enigmáticas «cajas negras» en «cajas blancas» transparentes y comprensibles. Al pasar de la simple observación de correlaciones a la comprensión de mecanismos causales, esta investigación nos proporciona un lenguaje para dialogar con nuestros sistemas de IA, para entender sus procesos internos y predecir su comportamiento.
Las implicaciones tecnológicas son inmensas. Si podemos comprender las leyes de escala que rigen la generalización, podremos diseñar procesos de entrenamiento mucho más eficientes. En lugar de gastar ingentes cantidades de recursos computacionales esperando que el grokking ocurra por casualidad, podríamos ser capaces de inducirlo, de guiar a los modelos directamente hacia las condiciones óptimas para el aprendizaje profundo, construyendo sistemas más robustos, fiables y económicos.
Finalmente, la relevancia social de este conocimiento es innegable. A medida que los sistemas de IA se integran cada vez más en el tejido de nuestra sociedad, tomando decisiones que afectan nuestras vidas, finanzas y salud, la capacidad de entender, predecir y controlar sus procesos de aprendizaje deja de ser un lujo académico para convertirse en un requisito indispensable para la seguridad y la confianza. Un modelo que no podemos entender es un modelo en el que no podemos confiar plenamente.
El trabajo de Yuandong Tian y su marco Li₂ no es la respuesta final, pero sí una pieza fundamental de este inmenso rompecabezas. Nos recuerda que el camino hacia una inteligencia artificial verdaderamente avanzada y beneficiosa no reside únicamente en construir modelos más grandes y potentes, sino en descifrar las leyes fundamentales del aprendizaje que los gobiernan. Esta investigación nos ofrece un atisbo de un futuro en el que la ciencia de la IA no solo crea artefactos inteligentes, sino que también comprende la naturaleza misma de la inteligencia.

Referencias
Abramov, R., Steinbauer, F., & Kasneci, G. (2025). Grokking in the wild: Data augmentation for real-world multi-hop reasoning with transformers.
Doshi, D., Das, A., He, T., & Gromov, A. (2023). To grok or not to grok: Disentangling generalization and memorization on corrupted algorithmic datasets.
Doshi, D., He, T., Das, A., & Gromov, A. (2024). Grokking modular polynomials.
Huang, Y., Hu, S., Han, X., Liu, Z., & Sun, M. (2024). Unified view of grokking, double descent and emergent abilities: A perspective from circuits competition.
Jordan, K., Jin, Y., Boza, V., You, J., Cesista, F., Newhouse, L., & Bernstein, J. (2024). Muon: An optimizer for hidden layers in neural networks.
Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., & Dean, J. (2013). Distributed representations of words and phrases and their compositionality. Advances in neural information processing systems, 26.
Millidge, B. (2022). Grokking ‘grokking’.
Mirzadeh, I., Alizadeh, K., Shahrokhi, H., Tuzel, O., Bengio, S., & Farajtabar, M. (2024). Gsm-symbolic: Understanding the limitations of mathematical reasoning in large language models.
Mohamadi, M. A., Li, Z., Wu, L., & Sutherland, D. J. (2024). Why do you grok? a theoretical analysis of grokking modular addition.
Nguyen, A., & Reddy, G. (2025). Differential learning kinetics govern the transition from memorization to generalization during in-context learning. In The Thirteenth International Conference on Learning Representations.
Power, A., Burda, Y., Edwards, H., Babuschkin, I., & Misra, V. (2022). Grokking: Generalization beyond overfitting on small algorithmic datasets.
Rubin, N., Seroussi, I., & Ringel, Z. (2024). Grokking as a first order phase transition in two layer networks. ICLR.
Shutman, M., Louidor, O., & Tessler, R. (2025). Learning words in groups: fusion algebras, tensor ranks and grokking.
Thilak, V., Littwin, E., Zhai, S., Saremi, O., Paiss, R., & Susskind, J. (2022). The slingshot mechanism: An empirical study of adaptive optimizers and the grokking phenomenon.
Tian, Y. (2023). Understanding the role of nonlinearity in training dynamics of contrastive learning. In The Eleventh International Conference on Learning Representations.
Provable scaling laws of feature emergence from learning dynamics of grokking
Tian, Y. (2025). Provable scaling laws of feature emergence from learning dynamics of grokking. Arxiv 2509.21519.
Walker, T., Humayun, A. I., Balestriero, R., & Baraniuk, R. (2025). Grokalign: Geometric characterisation and acceleration of grokking.
Wang, B., Yue, X., Su, Y., & Sun, H. (2024a). Grokked transformers are implicit reasoners: A mechanistic journey to the edge of generalization.
Xu, Z., Wang, Y., Frei, S., Vardi, G., & Hu, W. (2023). Benign overfitting and grokking in relu networks for xor cluster data.
Zhao, J., Zhang, Z., Chen, B., Wang, Z., Anandkumar, A., & Tian, Y. (2024). Galore: Memory-efficient Ilm training by gradient low-rank projection. ICML.



