Desde los albores de la revolución computacional, optimizar ha sido sinónimo de traducir problemas complejos en ecuaciones, restricciones y códigos que puedan ser resueltos por algoritmos. La investigación operativa y el modelado de optimización permiten planificar rutas de transporte, asignar recursos humanos, diseñar redes de distribución o maximizar beneficios bajo limitaciones. A pesar de su relevancia, esta disciplina ha quedado durante décadas en manos de expertos capaces de interpretar un enunciado y convertirlo en un modelo matemático.
La irrupción de los modelos de lenguaje de gran tamaño (LLM) brindó una salida novedosa: si una máquina puede resumir un texto, traducir idiomas o responder preguntas, ¿por qué no enseñarle a formular modelos de programación lineal a partir de una descripción en lenguaje natural?
Diversos esfuerzos han probado esta idea con resultados sorprendentes, pero siempre bajo un mismo paradigma: recopilar miles de pares problema‑solución y entrenar al modelo para que aprenda a imitar esas respuestas. Es lo que los autores de «CALM < BEFORE THE STORM W: unlocking native reasoning for optimization modeling» llaman generación no reflexiva.
El trabajo que motiva este artículo propone una ruptura con esa estrategia. Aprovecha el surgimiento de los llamados Large Reasoning Models (LRM), versiones de los LLM que poseen una habilidad intrínseca para razonar en múltiples pasos durante un mismo proceso de inferencia.
Estos sistemas son capaces de pensar, probar ideas, corregirse y continuar, algo semejante a la forma en que un investigador humano ajusta su razonamiento al obtener retroalimentación. La pregunta central que plantean los autores es si se puede explotar esa capacidad nativa de razonamiento para transformar la manera en que abordamos las tareas de modelado de optimización. La respuesta se articula en torno a dos conceptos: CALM y STORM.
El primero es un marco de adaptación que corrige suavemente la trayectoria de razonamiento de un LRM mediante intervenciones mínimas y a través del acceso al código de un solver. El segundo es el resultado de aplicar ese marco a un modelo de cuatro mil millones de parámetros, logrando un desempeño equiparable al de un gigante de seiscientos setenta y un mil millones de parámetros en varias pruebas estándar de optimización.
Este artículo desglosa el contenido del paper y lo presenta con un tono divulgativo, narrativo y riguroso. A lo largo de las siguientes secciones se explorarán los antecedentes de la automatización del modelado, se explicará por qué la estrategia tradicional encuentra sus límites cuando se enfrenta a modelos que razonan por sí mismos, se describirá detalladamente la anatomía de CALM y la formación de STORM, se revisarán los resultados experimentales y se discutirán las implicaciones sociales y científicas de este avance. La conclusión invita a reflexionar sobre el lugar que ocupará la inteligencia artificial en el descubrimiento de modelos matemáticos y sobre cómo podemos convertirla en aliada de quienes gestionan problemas reales.
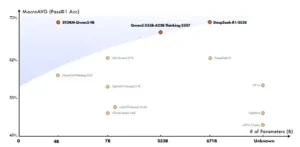
Panorama de rendimiento frente a tamaño del modelo para modelado de optimización.
De los LLM a los LRM: la promesa y la trampa
El desarrollo de modelos de lenguaje ha transformado tareas lingüísticas de forma radical, pero su aplicación a la investigación operativa tiene particularidades. Los primeros sistemas capaces de formular modelos recibieron nombres como ORLM, LLMOPT, OptMath o Solver‑Informed RL. Todos funcionan a partir del mismo principio: se construye un gran conjunto de datos con descripciones de problemas y sus soluciones en forma de código que llamará a un solver. El modelo aprende a asociar la narración con un bloque de Python donde se definen variables, se establecen restricciones y se llama a la biblioteca PuLP u otra herramienta de optimización.
Al final, se evalúa si el valor objetivo obtenido está dentro de un error relativo predefinido respecto a la solución real. Estas colecciones de pares problema‑solución se denominan datasets no reflexivos porque no contienen el hilo de pensamiento que une la pregunta con la respuesta; son, en cierto sentido, recetas negras que el modelo repite sin comprender su lógica interna.
La aparición de los LRMs obligó a repensar esta estrategia. Estos modelos, pertenecientes a familias como Qwen o DeepSeek, tienen la capacidad de razonar de manera iterativa durante la inferencia. No producen una salida en un solo pase; en cambio, generan líneas de razonamiento, ejecutan fragmentos de código, observan los resultados y ajustan su trayectoria. Este comportamiento, que el paper denomina patrón de razonamiento nativo, los hace aptos para tareas donde la retroalimentación incremental es clave, como la optimización.
No obstante, al aplicarles la misma técnica de ajuste con datos no reflexivos, los autores observaron un fenómeno curioso: el desempeño mejoraba en tareas sencillas, pero se desplomaba en los casos complejos. El modelo, forzado a seguir una rutina rígida, abandonaba su estilo reflexivo y se convertía en un generador lineal de código, perdiendo la habilidad de pensar paso a paso.
Para comprender la magnitud del problema, los investigadores realizaron un estudio piloto en el que tomaron un LRM base y lo fine‑tunearon con un conjunto de datos no reflexivo. Los resultados reflejan un crecimiento de la precisión en benchmarks simples como MAMO‑Easy, pero una caída abrupta en pruebas complejas como IndustryOR y OptMath. La explicación sugerida es que el entrenamiento obliga al modelo a reemplazar su razonamiento iterativo por una salida plana y sin introspección. Así, se inicia la exploración de cómo preservar las capacidades de razonamiento y corregir sus errores en lugar de anularlas.
¿Dónde se equivocan los LRMs? Taxonomía de fallos
Al reconocer que el talento de un LRM para razonar puede degradarse si se lo adiestra de manera inadecuada, el siguiente paso fue analizar sus errores. Los autores diseñaron un protocolo en el que un equipo humano con formación en investigación operativa solicitó a un LRM que resolviera un conjunto diverso de problemas. Luego, los expertos examinaron sus soluciones, anotaron cada error, los agruparon y sintetizaron una lista de siete tipos de fallos recurrentes. Este proceso se explica con detalle en el texto, pero su esencia reside en que la mayoría de las equivocaciones se pueden clasificar en dos grandes categorías conceptuales.
-
Desconfianza en la utilización del código: en algunos casos, el modelo intenta realizar cálculos manuales o escribe fragmentos de código redundantes en lugar de apoyarse en la potencia del solver. Este comportamiento indica que el sistema no confía plenamente en las herramientas externas y recurre a soluciones parciales e ineficientes.
-
Falta de conocimiento experto: en otros errores, el razonamiento se rompe porque el modelo no incorpora conceptos fundamentales de la investigación operativa. Se observan formulaciones matemáticas erróneas, restricciones faltantes o implementaciones incorrectas de la lógica del problema. Aquí la carencia es de dominio: al modelo le faltan destrezas propias de un analista humano.
La importancia de esta taxonomía no reside solo en nombrar los fallos, sino en comprender que cada categoría demanda una intervención distinta. La desconfianza en el código se combate redirigiendo al modelo hacia el uso del solver, mientras que la falta de conocimiento se aborda con recordatorios conceptuales. Además, los autores cuantificaron la presencia de estos errores en distintos benchmarks y descubrieron que en problemas sencillos predominan las fallas de confianza, mientras que en los complejos emerge la carencia de pericia en la investigación operativa. Esta observación guiará el diseño de las intervenciones correctivas.
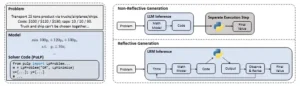
a) Un ejemplo de modelado de optimización b) Comparación de paradigmas de razonamientoen el modelado de optimización automatizada.
Ilustraciones de paradigmas de razonamiento y modelado de optimización.
CALM: corregir sin anular el pensamiento
El núcleo del paper es el marco CALM, sigla en inglés de Corrective Adaptation with Lightweight Modification. Su objetivo es preservar el razonamiento nativo del modelo mientras se corrigen sus desviaciones. Para lograrlo, los autores imaginan un sistema formado por dos agentes: el Razonador, que es el propio LRM, y el Interventor, un experto que supervisa su razonamiento y lo corrige mínimamente cuando detecta un error. El proceso ocurre dentro de un entorno que permite al modelo ejecutar código y obtener resultados.
La secuencia es así: el Razonador produce su primera aproximación de solución, el Interventor la revisa, identifica un error, inyecta un comentario o hint que reorienta la trayectoria, y el Razonador retoma la tarea integrando esa sugerencia. Se repite hasta que el Interventor considera que la solución es correcta o hasta que se alcanza un número máximo de intervenciones.
Lo interesante es que las intervenciones son muy ligeras: en promedio modifican menos del 2,6 % de los tokens generados. Un ejemplo típico se da cuando el LRM intenta resolver manualmente un problema de asignación. El Interventor agrega una línea que dice «tal vez puedo usar la biblioteca pulp y dejar que el solver encuentre la solución óptima». Con solo esa pista, el modelo evita calcular a mano y utiliza la herramienta adecuada.
Otro caso, en el que el modelo olvida que las variables que representan carros deben ser enteras, se corrige con la sugerencia «un número fraccionario de carros no es práctico, quizá falta una restricción de integridad». Cada intervención se dirige a un fallo concreto, sin reescribir la solución de manera total. De este modo, se preserva la estructura de pensamiento original y se lo fortalece con sugerencias puntuales.
CALM no solo corrige, sino que también sirve como generador de datos de alta calidad. Cada vez que el proceso termina con éxito, se guarda la secuencia completa de razonamiento y se marca como un «hallazgo dorado». Solo aquellas trayectorias que son correctas y están libres de errores, según el criterio del Interventor, se utilizan para entrenar el modelo en la siguiente fase. Esta selección rigurosa filtra la información basura y crea una base confiable para el aprendizaje supervisado.
El corpus de trayectorias doradas recopiladas mediante CALM alimenta un proceso de entrenamiento en dos etapas. La primera es un ajuste supervisado clásico, donde el modelo aprende a replicar el razonamiento curado. La meta no es alcanzar de inmediato la máxima puntuación, sino adaptar sus hábitos sin forzar un cambio brusco en su estilo. Esta etapa, llamada soft adaptation, actúa como un calibrador: corrige tics y modera las desviaciones sin destruir la estructura interna del razonamiento.
La segunda etapa utiliza aprendizaje por refuerzo. Ahora el modelo interactúa con el entorno ejecutando código hasta cuatro veces por problema, recibe una recompensa binaria si su solución está dentro de cierto margen de error y ajusta sus parámetros para maximizar ese premio. Los autores emplean el algoritmo Group Relative Policy Optimization, una variante del Proximal Policy Optimization adaptada a la interacción con solvers y con un número limitado de ejecuciones.
Esta fase se compara en el paper con la llegada de la tormenta: es la parte del entrenamiento en la que el modelo convierte las correcciones suaves en habilidades autónomas. Mientras que la adaptación supervisada es un susurro que dice «por aquí», el aprendizaje por refuerzo es un vendaval que lo empuja hasta alcanzar su máximo potencial.
STORM: un gigante en miniatura
El fruto de este pipeline es STORM, acrónimo de Smart Thinking Optimization Reasoning Model. Se trata de un LRM con cuatro mil millones de parámetros, entrenado sobre el marco CALM y luego pulido con aprendizaje por refuerzo. Su desempeño se mide utilizando cinco benchmarks ampliamente aceptados en la comunidad: NL4Opt, MAMO‑Easy, MAMO‑Complex, IndustryOR y OptMath. Estos conjuntos de pruebas abarcan desde tareas sencillas de programación lineal hasta problemas industriales complejos y casos matemáticos avanzados.
El artículo compara a STORM con una lista exhaustiva de modelos que incluyen sistemas cerrados como GPT‑3.5‑Turbo y GPT‑4, LRMs gigantes como DeepSeek‑R1‑0528 (671B) o Qwen3‑235B‑Thinking‑2507, métodos basados en agentes como Chain‑of‑Experts y OptiMUS, y enfoques de aprendizaje como ORLM, LLMOPT, OptMath o SIRL. La métrica principal es la precisión pass@1, es decir, la probabilidad de que el modelo produzca una solución correcta en el primer intento. Para reducir la varianza en la generación, cada problema se evalúa con ocho muestras y se limita el número de ejecuciones de código por trayectoria.
Los resultados son contundentes: STORM, con apenas cuatro mil millones de parámetros, alcanza un promedio de precisión del 68,9 % en los cinco benchmarks, superando cómodamente al modelo base (57,1 %) y empatando o mejorando el desempeño de modelos gigantes como DeepSeek‑R1‑0528. El salto más dramático se observa en MAMO‑Complex, donde la precisión aumenta 23,8 puntos porcentuales. Además, STORM marca un nuevo estado del arte en esta categoría, demostrando que una arquitectura pequeña con un entrenamiento inteligente puede competir con sistemas cientos de veces más grandes.
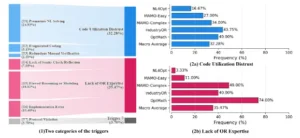
Categorización y distribución de los desencadenantes. La imagen de la izquierda (1) muestra la frecuencia macropromedio de cada desencadenante, agrupando los primeros seis en dos categorías principales. La imagen de la derecha (2a y 2b) detalla la distribución de frecuencias de estas dos categorías principales en los parámetros evaluados.
El valor de la selección y la poda: lo que revela el análisis
Para entender por qué el enfoque funciona, los autores realizan un estudio de ablación que separa los efectos de cada etapa del entrenamiento. Descubren que la adaptación supervisada actúa como un calibrador que mejora ligeramente la precisión y, más importante aún, evita la degradación observada cuando se usan datos no reflexivos.
Por sí sola, no produce el salto que se busca, pero prepara el terreno para la siguiente fase. El aprendizaje por refuerzo, en cambio, es el motor que impulsa el salto de 58,7 % a 68,9 % en la precisión macro. En palabras de los investigadores, el modelo pasa de un estado de calma a una tormenta de mejoras.
Otro análisis deconstruye el proceso de curación de datos. De los 549 ejemplos generados inicialmente, solo 443 sobrevivieron a un filtro que exigía una respuesta correcta. Tras la etapa de intervenciones y la aplicación de criterios de perfección, apenas 112 ejemplos se consideraron dignos de entrenar al modelo. Aunque esta selección parece drástica, se justifica porque su calidad eleva la tasa de éxito del 64,5 % al 80,7 % y reduce la longitud media de las respuestas en cerca de 2.600 tokens. Esto demuestra que lo importante no es la cantidad de datos, sino su pertinencia y pureza.
Finalmente, un experimento controlado compara el aprendizaje por refuerzo iniciado con trayectorias curadas frente al iniciado con secuencias sin intervención. El primer enfoque conduce a un aprendizaje más rápido, con curvas de precisión que suben de manera estable y alcanzan un techo alto, mientras que el segundo avanza con lentitud y termina muy por debajo.
El análisis del comportamiento revela que los modelos entrenados con CALM aumentan progresivamente el uso de bloques de código y reducen la longitud de sus respuestas, sustituyendo cálculos verbales por ejecuciones concisas. Se observa, además, un proceso de sanación en dos etapas: la adaptación supervisada reduce principalmente los errores de conocimiento, mientras que el aprendizaje por refuerzo corrige la desconfianza en el uso del código.
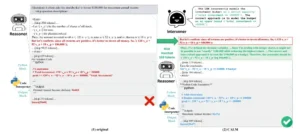
Un ejemplo representativo de la falla de falta de experiencia en OR. (1) El razonamiento nativo del modelo resulta en una formulación incorrecta del problema, lo que resulta en una respuesta incorrecta. (2) Por el contrario, el proceso guiado por CLAM corrige la formulación, permitiendo que el modelo encuentre la solución correcta.
Implicaciones tecnológicas y sociales
El desarrollo de sistemas como CALM y STORM introduce una nueva forma de colaboración entre la inteligencia artificial y la investigación operativa. En primer lugar, demuestra que la clave no es solo el tamaño de los modelos, sino la forma en que se entrenan. Con la guía adecuada y un enfoque en las capacidades de razonamiento propias, un modelo relativamente pequeño puede alcanzar resultados que antes se consideraban reservados para gigantes de cientos de miles de millones de parámetros.
Esto tiene implicaciones económicas: entrenar y ejecutar un modelo de cuatro mil millones consume menos energía, requiere menos infraestructura y puede ser más accesible para empresas o investigadores con recursos limitados.
En segundo lugar, la estrategia de intervenciones mínimas abre un camino para integrar conocimiento experto en los sistemas de forma elegante. En lugar de generar grandes datasets ad hoc, basta con que un experto añada sugerencias precisas allí donde el modelo se desvía. Este enfoque human‑in‑the‑loop puede ser adaptable a otros dominios donde las máquinas deban respetar procedimientos o reglamentos. Además, al fomentar que el modelo ejecute código real para verificar sus hipótesis, se introducen mecanismos de verificación que reducen la probabilidad de errores silenciosos.
Desde un punto de vista social, la capacidad de automatizar la creación de modelos de optimización plantea tanto oportunidades como desafíos. Por un lado, puede democratizar el acceso a herramientas de investigación operativa. Organizaciones pequeñas o autoridades locales podrían traducir problemas logísticos o de asignación en modelos de programación lineal sin necesidad de contratar a un experto, lo que agilizaría la toma de decisiones y la implementación de políticas eficientes.
Por otro lado, surge la necesidad de asegurar que estos sistemas sean transparentes y que sus sugerencias puedan ser auditadas. La reflexión de los autores sobre la necesidad de mantener la integridad de la supervisión humana es clave: si se abusa de la automatización sin filtros, el ecosistema académico y operativo podría inundarse de soluciones mal validadas o triviales.
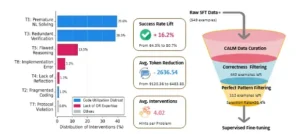
El motor de curación de datos CALM.
Un horizonte de posibilidades y límites
El éxito de CALM y STORM invita a imaginar aplicaciones más allá del modelado de optimización. La idea de preservar el razonamiento interno de un modelo y corregirlo con intervenciones ligeras podría aplicarse a sistemas que generan pruebas matemáticas, códigos de simulación o incluso argumentos legales. Siempre que exista un mecanismo de retroalimentación (un solver, un compilador, un verificador de teoremas), se puede concebir un Interventor que identifique errores y oriente al modelo.
Sin embargo, la estrategia tiene límites claros. El proceso de prueba y error es intensivo en recursos. En el paper se registran más de veinte mil horas de GPU para generar cinco mil ideas y validar unas mil cien, de las que apenas veintiuna dieron lugar a avances significativos. Esta tasa de éxito del uno al tres por ciento refleja la realidad de la investigación científica: la mayoría de las hipótesis fracasan.
Aunque la IA puede acelerar el ciclo, no lo elimina. En problemas donde cada experimento requiere semanas o meses, como la síntesis farmacéutica o el entrenamiento de modelos fundacionales gigantes, esta estrategia puede ser inviable. Además, el análisis de los fallos muestra que alrededor del sesenta por ciento de los fracasos se debe a errores de implementación, no de concepto, lo que pone en evidencia que la generación de código correcto sigue siendo un cuello de botella.
También se plantea una cuestión ética. Si un sistema puede generar artículos aparentemente creíbles y propuestas de modelos sin supervisión, podría inundar la literatura técnica de resultados dudosos. Los autores abogan por liberar solo parte del código y mantener cerrada la herramienta que compone los artículos, para proteger la integridad del ecosistema científico.
En paralelo, subrayan la importancia de que los modelos base posean alineación de seguridad para evitar usos dañinos; en sus pruebas, los agentes se negaron a generar virus informáticos, pero esta salvaguarda no puede darse por sentada en todas las implementaciones.
Últimas reflexiones
El viaje desde la identificación de las limitaciones de la adaptación tradicional hasta la construcción de un marco que desbloquea el razonamiento nativo de los modelos de lenguaje ofrece varias lecciones. La más obvia es que el tamaño no lo es todo: un modelo pequeño, entrenado con cuidado, puede superar a un gigante mal ajustado. La segunda es que la combinación de retroalimentación humana y aprendizaje automático es poderosa.
CALM no intenta reemplazar al experto, sino encapsular su conocimiento en intervenciones puntuales que guían al modelo. La tercera es que la automatización de la ciencia y de la ingeniería no ocurre en el vacío. Los sistemas que se construyen hoy tendrán efectos en cómo se enseña optimización, cómo se toman decisiones logísticas y cómo se desarrollan políticas públicas.
De cara al futuro, los autores proponen extender STORM a marcos de agentes más amplios, donde un modelo no solo formula un problema sino que interactúa con múltiples herramientas, equipos y fuentes de datos. El objetivo es crear sistemas que puedan asesorar a analistas humanos, sugerir estrategias y adaptarse a contextos dinámicos. Lograrlo requiere superar el desafío de la implementación robusta y asegurar que el comportamiento del modelo siga siendo legible y controlable.
Mientras tanto, el trabajo de CALM < BEFORE THE STORM W marca un hito al demostrar que la inteligencia artificial puede aprender a pensar como un científico de la optimización, con un poco de ayuda de aquellos que ya dominan la disciplina.
Referencias
Achiam, J., Adler, S., Agarwal, S., Ahmad, L., Akkaya, I., et al. (2023). GPT‑4 technical report.
AhmadiTeshnizi, A., Gao, W., & Udell, M. (2024). OptiMUS: Scalable optimization modeling with (MI) LP solvers and large language models.
Chen, Y., Xia, J., Shao, S., Ge, D., & Ye, Y. (2025). Solver‑informed reinforcement learning: Grounding large language models for authentic optimization modeling.
Huang, C., Tang, Z., Hu, S., Jiang, R., Zheng, X., Ge, D., Wang, B., & Wang, Z. (2025). ORLM: A customizable framework in training large models for automated optimization modeling.
Jiang, C., Shu, X., Qian, H., Lu, X., Zhou, J., Zhou, A., & Yu, Y. (2024). LLMOPT: Learning to define and solve general optimization problems from scratch.
Li, C., Tang, Z., Li, Z., Xue, M., Bao, K., Ding, T., Sun, R., Wang, B., Wang, X., Lin, J., et al. (2025). Cort: Code‑integrated reasoning within thinking.
Li, C., Xue, M., Zhang, Z., Yang, J., Zhang, B., Wang, X., Hui, B., Lin, J., & Liu, D. (2025). Start: Self‑taught reasoner with tools.
Lu, H., Xie, Z., Wu, Y., Ren, C., Chen, Y., & Wen, Z. (2025). OptMath: A scalable bidirectional data synthesis framework for optimization modeling.
Qwen Team. (2025). Qwen3 technical report.
Ramamonjison, R., Yu, T., Li, R., Li, H., Carenini, G., Ghad‑dar, B., He, S., Mostajabdaveh, M., Banitalebi‑Dehkordi, A., & Zhou, Z. (2023). NL4Opt competition: Formulating optimization problems based on their natural language descriptions.
Tang, Z., Ye, Z., Huang, C., Huang, X., Li, C., Li, S., Chen, G., Yan, M., Wang, Z., Zha, H., Liu, D., & Wang, B. (2025). CALM < BEFORE THE STORM W: unlocking native reasoning for optimization modeling.



