Cada año, las mentes matemáticas más agudas del planeta, jóvenes prodigios que aún no han pisado la universidad, se congregan para enfrentarse a un desafío de proporciones legendarias: la Olimpiada Internacional de Matemáticas (IMO). No es una simple competición; es el crisol definitivo del ingenio, la creatividad y la intuición matemática. Desde su inauguración en Rumanía en 1959, la IMO se ha consolidado como el Everest del pensamiento abstracto, un certamen donde los problemas no se resuelven con meros cálculos, sino con saltos de imaginación y una elegancia conceptual que durante décadas pareció ser un bastión inexpugnable, exclusivamente humano. Los seis problemas de la olimpiada, repartidos en dos jornadas extenuantes, están diseñados para explorar los límites de la creatividad, exigiendo a los participantes no solo conocer teoremas, sino inventar nuevas formas de verlos.
En este escenario de pura proeza intelectual, el verano de 2025 marcó un punto de inflexión histórico. Un anuncio sacudió los cimientos de la comunidad científica y tecnológica: un sistema de inteligencia artificial, bautizado con el nombre del padre de la lógica occidental, Aristóteles, había alcanzado un rendimiento equivalente a una medalla de oro. Desarrollado por un equipo de investigadores en la empresa Harmonic, este agente digital resolvió de manera impecable cinco de los seis problemas del certamen.
El hito es comparable a la victoria de la supercomputadora Deep Blue sobre Garri Kaspárov en ajedrez o al triunfo de AlphaGo sobre Lee Sedol en el ancestral juego del Go. Sin embargo, lo que logró Aristóteles es, en muchos sentidos, más profundo. No se trataba de dominar un juego con reglas finitas, por complejo que fuera, sino de aventurarse en el terreno ilimitado y etéreo del razonamiento matemático puro, el mismo que ha dado forma a la ciencia y la civilización.
Para comprender la magnitud de esta hazaña, es fundamental desentrañar la dualidad que define el pensamiento matemático y que Aristóteles ha logrado dominar. Por un lado, existe el razonamiento informal. Pensemos en él como la intuición de un gran chef. Es el proceso creativo, a veces caótico y siempre brillante, que da lugar a una nueva receta. El chef combina sabores en su mente, imagina texturas, esboza una idea general y confía en su experiencia para saber qué funcionará. Este es el tipo de pensamiento que un matemático humano utiliza para trazar una estrategia, para tener una corazonada sobre el camino que podría llevar a una solución. Es un lenguaje de ideas, de borradores y de planes de alto nivel.
Por otro lado, está el razonamiento formal. Si la intuición del chef es la idea, el razonamiento formal es la receta final, escrita con una precisión absoluta y sin ambigüedades. Es una secuencia de instrucciones tan meticulosa que cualquiera, o cualquier máquina, puede seguirla al pie de la letra y obtener exactamente el mismo resultado, una y otra vez. En matemáticas, este es el lenguaje de la demostración rigurosa, una cadena de deducciones lógicas donde cada paso se sigue ineludiblemente del anterior. La genialidad de Aristóteles reside precisamente en su capacidad para ser, simultáneamente, el chef creativo y el meticuloso escritor de recetas.
El guardián de esta verdad absoluta, el lenguaje en el que Aristóteles debe escribir sus «recetas», es un sistema llamado Lean 4. Lean no es un lenguaje de programación cualquiera; es un asistente de demostración, una especie de árbitro incorruptible de la lógica. Una demostración escrita en Lean no es un argumento que busca persuadir a un humano, sino una construcción matemática que un ordenador puede verificar con certeza absoluta. Si hay un solo paso en falso, un pequeño salto lógico no justificado, el sistema lo rechaza. Esta es la garantía de Aristóteles contra las «alucinaciones», esas respuestas elocuentes y plausibles, pero fundamentalmente incorrectas, que a menudo plagan a los grandes modelos de lenguaje. La condición para que Aristóteles resolviera un problema no era simplemente encontrar la respuesta, sino producir una demostración completa y verificable por máquina en Lean 4, sin fisuras ni atajos.
Este requisito establece una diferencia crucial con otros logros recientes. En la misma olimpiada, sistemas de gigantes como Google DeepMind y OpenAI también anunciaron resultados de medalla de oro, pero sus soluciones fueron presentadas en lenguaje natural, como las escribiría un estudiante, y fueron evaluadas por jueces humanos. Aunque impresionante, este enfoque tiene una limitación fundamental: verificar una demostración matemática compleja en lenguaje natural puede ser una tarea casi tan ardua y propensa a errores como crearla. Las soluciones de Aristóteles, en cambio, pertenecen a una categoría superior de certeza. No dependen de la interpretación humana, sino de la fría e implacable lógica de una máquina. Son pruebas, en el sentido más puro de la palabra.
El éxito de Aristóteles, por tanto, no es solo una proeza de resolución de problemas. Representa un avance fundamental en la propia naturaleza de la inteligencia artificial. Al fusionar la intuición de estilo humano con un rigor mecánico e infalible, este sistema ha creado un modelo sinérgico que podría sacarnos de la era de la «caja negra» en el razonamiento de las máquinas. Durante años, una de las mayores críticas a las IA ha sido la opacidad de su proceso de pensamiento; generan respuestas sin que podamos auditar completamente su lógica.
Aristóteles ofrece una solución elegante: permite que la IA explore y cree libremente en el espacio de las ideas informales, pero exige que el producto final sea un artefacto de lógica transparente, un cristalino y auditable rastro de razonamiento puro. Este sistema no solo ha conquistado la olimpiada; ha inaugurado una nueva era de confianza y fiabilidad en la búsqueda del conocimiento, abriendo la puerta a una colaboración sin precedentes entre la mente humana y la inteligencia artificial en la gran aventura del descubrimiento científico.
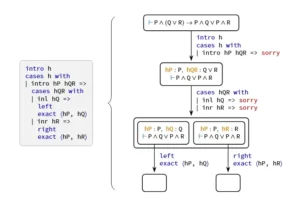
Una demostración formal de una dirección de la distributividad de AND sobre OR, junto con una realización como parte de un hiperárbol de búsqueda. Los bordes del árbol despliegan la demostración como una serie de acciones, mientras que sus nodos registran la evolución del estado Lean. La táctica del segundo caso conduce a dos estados separados que se resuelven de forma independiente. Las hojas vacías indican que no quedan objetivos, por lo que la afirmación raíz está probada.
El nacimiento de un pensador híbrido: la arquitectura de Aristotle
El extraordinario rendimiento de Aristóteles no es producto de un único algoritmo monolítico, sino de una arquitectura sofisticada y modular, una suerte de equipo de especialistas cognitivos que trabajan en perfecta sincronía. Este diseño tripartito es la clave de su versatilidad, permitiéndole combinar la planificación estratégica con la ejecución lógica y el uso de herramientas especializadas. Cada componente tiene una función distinta, pero es su interacción lo que da lugar a una capacidad de razonamiento que supera la suma de sus partes.
El primer pilar, el corazón lógico del sistema, es su motor de búsqueda de pruebas en Lean. Este componente es el obrero incansable, el maestro artesano encargado de construir la demostración final, ladrillo a ladrillo. Su tarea comienza cuando recibe un «boceto de prueba», que es esencialmente un plan de ataque con los pasos principales definidos, pero con los detalles lógicos aún por rellenar. Estos huecos en el razonamiento están marcados en el código con la instrucción sorry, una señal para que el motor de búsqueda entre en acción y complete la cadena deductiva.
Para navegar por el laberinto casi infinito de posibles pasos lógicos, este motor utiliza una técnica avanzada conocida como Búsqueda de Grafo de Monte Carlo (MCGS). Para entender su funcionamiento, podemos imaginar a un explorador encargado de encontrar un camino a través de una selva inmensa y desconocida. Un explorador ingenuo podría intentar recorrer cada sendero posible, una tarea que le llevaría una eternidad. El explorador de Monte Carlo, en cambio, es mucho más astuto.
En lugar de explorar a fondo cada camino, primero envía miles de drones de reconocimiento que realizan vuelos rápidos y aleatorios (las «simulaciones» o «playouts») a través de diferentes secciones de la selva. Estos vuelos le proporcionan una visión estadística, un mapa de probabilidades que le indica qué áreas parecen más prometedoras para encontrar una salida. Con esta información, el explorador puede enfocar su energía y recursos en investigar a fondo solo los senderos con mayor potencial.
De manera análoga, el algoritmo de Aristóteles no analiza exhaustivamente cada posible táctica de Lean. Realiza miles de simulaciones rápidas para estimar qué secuencias de pasos lógicos tienen más probabilidades de cerrar una demostración y luego concentra su poder computacional en esas vías prometedoras. Además, su implementación como una búsqueda de «grafo» en lugar de un simple «árbol» es aún más eficiente, ya que le permite reconocer si diferentes secuencias de movimientos conducen al mismo estado lógico, evitando así explorar el mismo terreno dos veces. La «intuición» de este explorador digital es proporcionada por un gigantesco modelo de lenguaje de tipo transformer, que predice las tácticas más adecuadas y evalúa el valor de los diferentes estados de la prueba, guiando la búsqueda de manera inteligente.
El segundo pilar de la arquitectura es el estratega creativo: un sistema de razonamiento informal basado en lemas. Si el motor de búsqueda es el obrero que coloca los ladrillos, este componente es el arquitecto que diseña el edificio. Su función es emular una de las habilidades más poderosas de un matemático humano: la capacidad de descomponer un problema abrumadoramente complejo en una serie de subproblemas más pequeños y manejables, conocidos como lemas.
Enfrentado a un teorema de la IMO, este sistema no intenta resolverlo de un solo golpe. En su lugar, activa un proceso iterativo de planificación y traducción. Primero, genera una demostración informal en lenguaje natural, como la que un matemático podría garabatear en una pizarra. A continuación, analiza este texto y lo descompone en una secuencia lógica de lemas. El siguiente paso es uno de los más cruciales: la «autoformalización», que consiste en traducir el enunciado de cada lema del lenguaje humano al lenguaje preciso y riguroso de Lean. Este proceso de traducción es imperfecto y a menudo introduce errores.
Aquí es donde entra en juego un bucle de retroalimentación vital: el sistema envía los lemas formalizados al compilador de Lean y utiliza los mensajes de error recibidos para corregir y refinar sus propias traducciones. Si tras un intento la demostración principal sigue sin resolverse, el sistema analiza qué lemas consiguió probar y cuáles no, y utiliza esa información para revisar su estrategia, proponiendo nuevos lemas o desglosando los existentes en pasos aún más pequeños. Es un mecanismo de autocorrección robusto que combina la flexibilidad del lenguaje natural con la disciplina de la lógica formal.
El tercer y último componente es el especialista veloz: un solucionador de geometría llamado Yuclid. Este subsistema es la herramienta de alta precisión del equipo, un instrumento diseñado específicamente para un tipo de tarea: los problemas de geometría plana. Inspirado en el sistema AlphaGeometry de Google, Yuclid opera fuera del entorno principal de Lean, utilizando un enfoque híbrido que combina una base de datos deductiva de reglas geométricas con un potente motor de razonamiento algebraico. Lo que distingue a Yuclid es su extraordinaria velocidad. Gracias a una serie de optimizaciones implementadas en el lenguaje de programación C++, es hasta 500 veces más rápido que sus predecesores. Este componente demuestra un principio fundamental en el diseño de inteligencias avanzadas: la sinergia entre un razonador generalista y herramientas especializadas y de alto rendimiento.
Observada en su conjunto, la arquitectura tripartita de Aristóteles trasciende la mera ingeniería de software para resolver problemas matemáticos; se revela como un modelo funcional de la propia cognición científica. El proceso refleja asombrosamente cómo trabajan los científicos humanos. Un investigador no se lanza directamente a realizar cálculos complejos. Primero, formula una hipótesis de alto nivel y un plan de investigación estratégico, un proceso análogo al razonamiento informal del generador de lemas de Aristóteles. A continuación, se sumerge en la fase de ejecución, realizando experimentos detallados o derivaciones lógicas para probar o refutar cada parte de su plan, un trabajo metódico que se asemeja a la búsqueda de pruebas formal del motor de Lean.
Finalmente, para tareas específicas, el científico utiliza instrumentos especializados, como un telescopio, un secuenciador de ADN o un colisionador de partículas, que son equivalentes funcionales al solucionador de geometría Yuclid. Esta correspondencia sugiere que los principios arquitectónicos de Aristóteles son generalizables. Un sistema similar podría diseñarse para la química, generando rutas de síntesis de moléculas (razonamiento informal) y verificándolas mediante simulaciones cuánticas (búsqueda formal), o para la biología, proponiendo hipótesis sobre el plegamiento de proteínas y poniéndolas a prueba con modelos predictivos especializados. Aristóteles, por lo tanto, no es solo un campeón de las olimpiadas; es un prototipo pionero de una arquitectura general para la inteligencia artificial aplicada al descubrimiento científico.
El arte de aprender a demostrar: el entrenamiento de Aristotle
La capacidad de Aristóteles para razonar a un nivel de élite no surgió de la nada. Es el resultado de un proceso de entrenamiento innovador y multifacético, un régimen de aprendizaje diseñado para forjar una intuición matemática a partir de datos y experiencia. En el núcleo de este proceso se encuentra una de las técnicas más potentes de la inteligencia artificial moderna: el aprendizaje por refuerzo.
Para entender el aprendizaje por refuerzo, podemos usar una analogía sencilla: adiestrar a una mascota con premios. Imaginemos que queremos enseñarle a un cachorro a sentarse. El cachorro, que es el «agente», prueba una acción en su «entorno». Si por casualidad se sienta, le damos un premio, una «recompensa» positiva. Si ladra o salta, no recibe nada, o quizás una corrección suave, un «castigo» o recompensa nula. A través de innumerables repeticiones de este ciclo de acción y recompensa, el cachorro aprende a asociar la acción de sentarse con un resultado positivo.
Con el tiempo, desarrolla una «política», una estrategia interna que le dice que la mejor acción a tomar cuando escucha la orden es sentarse, porque maximiza la probabilidad de recibir un premio. Aristóteles aprende de una manera conceptualmente similar. El «agente» es el modelo de IA, el «entorno» es el estado actual de una demostración matemática, y una «acción» es la aplicación de una táctica de Lean. Si la táctica elegida acerca la demostración a su conclusión, el sistema recibe una recompensa positiva. Si conduce a un callejón sin salida o a un estado lógicamente inválido, la recompensa es negativa o nula.
El razonamiento matemático formal resulta ser un campo de juego excepcionalmente fértil para este tipo de aprendizaje. A diferencia de otros dominios donde la recompensa puede ser subjetiva o tardía, aquí la retroalimentación es instantánea, objetiva e inequívoca. El compilador de Lean actúa como un juez perfecto: el código que representa un paso de la demostración o bien compila, lo que significa que el paso es lógicamente válido (recompensa), o no lo hace (castigo). No hay ambigüedad. Este ciclo de retroalimentación claro y rápido permite al sistema aprender de manera extraordinariamente eficiente. Este método, conocido como «iteración de experto», permite que el sistema se convierta en su propio maestro, aprendiendo continuamente de las demostraciones exitosas que él mismo descubre durante la búsqueda.
Sin embargo, para que este ciclo de aprendizaje sea efectivo, se necesita un vasto terreno de entrenamiento, un universo de problemas matemáticos sobre los que practicar. Aquí es donde el equipo de Harmonic se enfrentó a un desafío monumental: la gran mayoría del conocimiento matemático de la humanidad está escrito en lenguaje natural, en libros de texto y artículos científicos, no en el código formal que Aristóteles necesita para entrenar. Crear manualmente un conjunto de datos de este tamaño sería una tarea faraónica.
La solución fue tan ambiciosa como el propio sistema: desarrollaron un motor de «autoformalización». Este sistema es capaz de leer enunciados matemáticos en lenguaje natural y traducirlos automáticamente a la sintaxis precisa de Lean. Al procesar una inmensa biblioteca de conocimiento matemático, este motor generó el gigantesco conjunto de datos necesario para alimentar el insaciable apetito de aprendizaje del agente de refuerzo.
Quizás la faceta más fascinante e innovadora del régimen de entrenamiento de Aristóteles es una técnica conocida como Entrenamiento en Tiempo de Prueba (Test-Time Training o TTT). Si el aprendizaje por refuerzo es el entrenamiento a largo plazo, el TTT es la capacidad del sistema para «estudiar intensivamente» para un examen específico y particularmente difícil.
Pensemos en un estudiante humano que se enfrenta a un problema de la IMO. En su primer intento, fracasa. En lugar de rendirse, el estudiante no vuelve a estudiar todo el temario de matemáticas desde el principio. En cambio, analiza sus intentos fallidos, identifica sus errores conceptuales y las lagunas en su conocimiento específico para ese problema, y concentra su estudio en esas áreas concretas. Después de este período de preparación enfocada, lo intenta de nuevo, ahora mucho mejor preparado.
El TTT automatiza este proceso de aprendizaje adaptativo. Cuando Aristóteles se enfrenta a un problema complejo, primero realiza numerosos intentos para resolverlo, tanto a él como a los lemas que ha generado. En el proceso, acumula un registro detallado de sus esfuerzos, un conjunto de «trazas de búsqueda» que documentan sus éxitos y fracasos. Si no logra encontrar una solución, el sistema no descarta esta experiencia. Por el contrario, la trata como un valiosísimo conjunto de datos de entrenamiento temporal e hiperenfocado. Reentrena su propio modelo neuronal utilizando estas trazas de sus intentos recientes.
En esencia, se especializa a sí mismo sobre la marcha, adaptando sus redes neuronales a los patrones y dificultades únicos de ese problema en particular. Una vez completado este ciclo de auto-mejora, vuelve a intentar resolver el problema, pero esta vez con un «cerebro» recién optimizado para el desafío que tiene entre manos.
Esta capacidad de aprender durante el propio acto de razonar representa un cambio de paradigma fundamental. Los modelos de inteligencia artificial tradicionales son artefactos estáticos: se entrenan una vez en un conjunto de datos masivo y luego se despliegan con un conocimiento fijo. Su capacidad está congelada en el momento en que finaliza su entrenamiento. El TTT rompe este molde estático, transformando a Aristóteles en un sistema dinámico y adaptativo que aprende en tiempo de inferencia, es decir, mientras está trabajando activamente en un problema.
La implicación es profunda: el rendimiento de la IA ya no está estrictamente limitado por su entrenamiento inicial. Puede mejorar sus propias capacidades en respuesta directa a un desafío novedoso. Esto abre la puerta a la creación de inteligencias artificiales capaces de abordar problemas verdaderamente abiertos, aquellos para los que no existe un conjunto de datos de entrenamiento previo. El TTT proporciona un mecanismo para que un sistema de IA impulse su propio conocimiento y especialice sus habilidades en el contexto único del problema que enfrenta, un paso crucial hacia una inteligencia más general y autónoma.
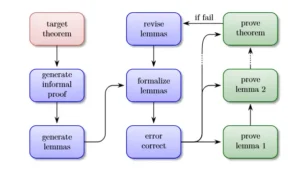
El teorema objetivo (rojo) se procesa mediante una secuencia de consultas en lenguaje natural (azul), lo que genera una serie de lemas que son procesados por el algoritmo de búsqueda (verde). Si el teorema permanece sin demostrar, se revisan los lemas no demostrados y se repite el procedimiento.
La coronación en la olimpiada: anatomía de una victoria
El escenario de la Olimpiada Internacional de Matemáticas de 2025 fue el campo de pruebas definitivo. Seis problemas, extraídos de las profundidades del álgebra, la teoría de números, la geometría y la combinatoria, esperaban a los contendientes. En este certamen, obtener una puntuación perfecta en cinco de ellos es el umbral para la medalla de oro, un logro reservado para una élite minúscula. Aristóteles cruzó ese umbral. Produjo soluciones formales, completas y verificadas para cinco de los seis problemas, tropezando únicamente en el sexto y último, un enigma de notoria dificultad que también resistió los asaltos de los demás sistemas de IA que compitieron. Un análisis detallado de las soluciones de Aristóteles a los problemas no geométricos revela no solo su poder, sino también la diversidad y sofisticación de sus estrategias de razonamiento.
- Problema 1: «Sunny lines» y la creatividad no humana
La demostración que Aristóteles produjo para este problema fue, según sus creadores, «diferente a la mayoría de las demostraciones humanas». El problema trataba sobre líneas que pasaban por puntos de una retícula dentro de un triángulo. Un enfoque humano típico se basaba en una intuición geométrica: el hecho de que una línea recta solo puede cruzar como máximo dos lados de un cuerpo convexo como un triángulo. Si bien esta idea es geométricamente obvia, su formalización rigurosa en Lean es engorrosa. Aristóteles, sin embargo, eludió por completo esta vía. En su lugar, encontró un camino puramente algebraico, una solución que estudiaba ciertas permutaciones sin puntos fijos, conocidas como «desarreglos», que estaban implícitamente ocultas en la estructura del problema. Su enfoque fue metódico y computacional, examinando casos hasta para encontrar un contraejemplo explícito, lo que le permitió descartar la construcción para todos los valores superiores. Este episodio es revelador: la IA no se limitó a imitar el pensamiento humano. Descubrió una ruta de solución genuinamente novedosa, quizás más elegante y ciertamente menos intuitiva para una mente humana, exhibiendo una forma de inteligencia que, aunque ajena, es indiscutiblemente correcta.
- Problema 3: «Bonza functions» y la invención de conceptos
Este problema requería caracterizar un tipo específico de funciones que satisfacían una particular relación de congruencia. Durante las primeras etapas de su exploración, Aristóteles comenzó a organizar su razonamiento en torno a un cierto conjunto de números primos, un concepto que finalmente formalizó en Lean con una definición auxiliar que denominó S. Este conjunto, definido como , no estaba sugerido en el enunciado del problema ni formaba parte de las estrategias humanas estándar. Sin embargo, se convirtió en una herramienta central en las demostraciones finales de varios lemas clave. Este acto de crear una nueva definición, de inventar un concepto auxiliar para simplificar y estructurar un problema complejo, es una de las señas de identidad del razonamiento matemático avanzado. Demuestra que Aristóteles no es un simple seguidor de reglas, sino que es capaz de un nivel superior de abstracción, estructurando el problema de una manera creativa para hacerlo más tratable.
- Problema 4: «Sums of three divisors» y el poder de la autocorrección
La solución a este problema, que trataba sobre secuencias infinitas de números regidas por una relación de recurrencia, se convirtió en un ejemplo paradigmático de la sinergia entre el razonamiento informal y la verificación formal. El argumento central que desarrolló Aristóteles era muy similar al de una solución humana típica. Sin embargo, el proceso que condujo a esa prueba fue un escaparate del poder de la formalización para detectar y corregir errores sutiles. En uno de los borradores informales generados por el sistema, apareció un fragmento de razonamiento defectuoso: «en este caso, . Si la secuencia entra en tal estado, se vuelve estrictamente decreciente. Para una secuencia infinita de enteros positivos, esto solo es posible si finalmente se vuelve constante». El texto confundía de manera sutil tres conceptos distintos: secuencias estrictamente decrecientes, secuencias débilmente decrecientes y secuencias que decrecen en algún punto. Este tipo de ambigüedad lingüística es emblemática de los desafíos que plantea la verificación de demostraciones generadas por IA en lenguaje natural. Un juez humano podría pasarla por alto. Sin embargo, durante la fase de autoformalización, la lógica implacable de Lean no lo hizo. Al intentar traducir la idea a un código riguroso, el sistema detectó la inconsistencia. Lejos de desechar el plan, Aristóteles reparó el error, preservando las ideas clave del borrador defectuoso pero rellenando sus lagunas lógicas. El resultado final no fue solo una demostración formalmente correcta, sino también un conjunto de comentarios informales corregidos, que proporcionaban una explicación en lenguaje natural precisa y validada de la lógica final.
- Problema 5: «Inekoalaty game» y la fluidez sofisticada
La solución a este problema de teoría de juegos, que requería identificar estrategias óptimas, mostró tanto la capacidad de invención conceptual de Aristóteles como la amplitud de su conocimiento técnico. Al igual que en el problema de las «Bonza functions», el sistema introdujo una definición auxiliar no sugerida por el enunciado: una función ![]() , que resultó ser un invariante útil durante la demostración. Más sorprendente aún fue su fluidez con conceptos matemáticos que, en principio, son innecesarios para resolver problemas de la IMO, los cuales están diseñados para ser accesibles con herramientas de secundaria. En una de sus primeras demostraciones, para probar un límite superior, Aristóteles utilizó cálculo diferencial, computando las derivadas de otra cantidad auxiliar para encontrar sus máximos. Aunque más tarde reemplazó esta prueba por una más directa, el hecho de que la considerara demuestra su acceso a un arsenal matemático muy amplio. Otro ejemplo fue su uso de la táctica
, que resultó ser un invariante útil durante la demostración. Más sorprendente aún fue su fluidez con conceptos matemáticos que, en principio, son innecesarios para resolver problemas de la IMO, los cuales están diseñados para ser accesibles con herramientas de secundaria. En una de sus primeras demostraciones, para probar un límite superior, Aristóteles utilizó cálculo diferencial, computando las derivadas de otra cantidad auxiliar para encontrar sus máximos. Aunque más tarde reemplazó esta prueba por una más directa, el hecho de que la considerara demuestra su acceso a un arsenal matemático muy amplio. Otro ejemplo fue su uso de la táctica filter_upwards. Esta es una herramienta relativamente oscura de la biblioteca Mathlib, utilizada en la manipulación de «filtros», un concepto abstracto de la topología que fundamenta la definición de límites. Aristóteles la empleó para demostrar que su función se aproximaba a . Este uso de técnicas avanzadas y especializadas ilustra su capacidad para desplegar un rango de conocimientos que va mucho más allá de lo esperado, seleccionando la herramienta más eficaz para el trabajo, sin importar cuán sofisticada sea.
Más allá de la competición: un nuevo colega para los matemáticos
El triunfo de Aristóteles en la Olimpiada Internacional de Matemáticas es mucho más que un hito en una competición. Señala el amanecer de una nueva era en la práctica de las matemáticas, donde la inteligencia artificial trasciende el papel de una mera calculadora para convertirse en un colaborador activo en la investigación. Incluso durante su fase de entrenamiento, antes de enfrentarse a los desafíos de la IMO, Aristóteles ya estaba demostrando su utilidad en contextos matemáticos genuinos, contribuyendo de manera significativa al cuerpo de conocimiento formalizado de la humanidad.
Su impacto más directo se ha sentido en Mathlib, la principal biblioteca de matemáticas formalizadas para el asistente de demostración Lean. Esta biblioteca es un proyecto comunitario colosal que busca construir un repositorio digital de teoremas y definiciones matemáticas verificadas por máquina. Durante su entrenamiento, Aristóteles identificó y demostró de forma autónoma varios teoremas importantes que faltaban en Mathlib, como el teorema de Niven, sobre las raíces racionales de funciones trigonométricas, y el teorema de Gauss-Lucas, que relaciona las raíces de un polinomio con las de su derivada. Además, contribuyó con numerosos lemas técnicos que fortalecieron la infraestructura lógica de la biblioteca. Estas no son meras soluciones a problemas de concurso; son contribuciones perdurables a un proyecto fundamental para el futuro de las matemáticas. Su capacidad no se detuvo ahí. Aristóteles también aportó lemas a otros proyectos de formalización de vanguardia, como el que lidera el medallista Fields Terence Tao para formalizar la conjetura de Polynomial Freiman-Ruzsa, un problema abierto en combinatoria aditiva.
Quizás la demostración más elocuente de su potencial como colega matemático provino de una prueba de fuego inusual: se le encomendó la tarea de procesar varios capítulos del libro de texto de análisis real de Terence Tao, que está siendo formalizado en Lean. El resultado fue asombroso. Aristóteles actuó como el asistente de investigación más diligente y preciso que se pueda imaginar. Descubrió cuatro ejercicios en el libro que, tal como estaban escritos, eran falsos, y para cada uno de ellos proporcionó contraejemplos explícitos que demostraban el error. Resolvió todas las demás proposiciones que se le presentaron, pero su contribución fue aún más sutil. En dos de los ejercicios, notó que una de las hipótesis que se les daba a los estudiantes era, de hecho, innecesaria para completar la demostración. Esta capacidad para identificar suposiciones redundantes es un signo de una profunda comprensión conceptual, no de una simple manipulación de símbolos. Este ejercicio demostró que Aristóteles puede actuar como un verificador de hechos sobrehumano, capaz de validar y depurar el trabajo matemático con una fiabilidad inalcanzable para una persona.
Para poner en perspectiva el avance que representa Aristóteles, es útil contrastar su enfoque con el de otros sistemas de IA que también alcanzaron un alto rendimiento en la IMO 2025. La diferencia fundamental radica en la naturaleza de sus soluciones y el método de su verificación.
| Característica | Aristotle (Harmonic) / Seed-Prover (ByteDance) | Gemini Deep Think (Google) / Sistema de OpenAI |
| Formato de la solución | Prueba formal en lenguaje Lean 4. | Prueba en lenguaje natural (inglés, como un humano). |
| Método de verificación | Compilación y verificación por máquina. Lógicamente infalible. | Evaluación por jueces humanos. Sujeto a error humano. |
| Fiabilidad | Absoluta. La prueba es matemáticamente garantizada. | Alta, pero no absoluta. Depende de la pericia y atención de los jueces. |
| Transparencia | Total. La prueba es una cadena de pasos lógicos explícitos. | Opaca. El «razonamiento» del modelo es un proceso de caja negra. |
| Implicación científica | Abre la puerta a la asistencia de IA en investigación rigurosa. | Demuestra capacidades de razonamiento avanzadas, pero con menor fiabilidad para la ciencia. |
Esta distinción es crucial. Mientras que las soluciones en lenguaje natural demuestran una impresionante capacidad de la IA para imitar el discurso matemático humano, las soluciones formales de Aristóteles representan un estándar de rigor completamente diferente. Ofrecen una certeza matemática que puede servir de base para futuras investigaciones, una roca sólida sobre la que se pueden construir nuevos conocimientos.
Hacia una nueva era de descubrimiento matemático
El logro de Aristóteles en la Olimpiada Internacional de Matemáticas no debe verse como un punto final, la culminación de una carrera entre la inteligencia humana y la artificial. Por el contrario, es un punto de partida, el anuncio de una nueva forma de hacer ciencia. Su éxito no proviene de un único algoritmo milagroso, sino de la elegante integración de dos modos de pensamiento: la planificación intuitiva, similar a la humana, y el rigor lógico e infalible de la máquina. Esta arquitectura híbrida es la que le confiere su poder y la que traza el camino a seguir.
Lejos de las visiones distópicas de una IA que reemplaza a los pensadores humanos, el futuro que Aristóteles sugiere es uno de simbiosis y colaboración. Los matemáticos y científicos podrán liberarse de la laboriosa y a menudo tediosa tarea de la verificación formal, un proceso donde un pequeño error puede invalidar meses de trabajo. Podrán delegar esta carga en asistentes de IA como Aristóteles, seguros de que cada paso lógico será examinado con una precisión sobrehumana. Esto les permitirá concentrarse en lo que los humanos hacen mejor: formular preguntas audaces, proponer conjeturas creativas, guiar la estrategia general de la investigación y dar sentido a los descubrimientos. La IA no será un rival, sino un socio indispensable, un explorador incansable de posibilidades lógicas, un verificador infalible e incluso una fuente de inspiración, capaz de sugerir caminos novedosos que una mente humana podría haber pasado por alto.
El impacto de este avance se extenderá mucho más allá de las fronteras de las matemáticas puras. Los principios demostrados por Aristóteles, la combinación de modelos generativos para la ideación con sistemas de verificación formal para la validación, ofrecen un marco robusto para la aplicación de la IA en cualquier campo donde la corrección y la fiabilidad sean primordiales. Pensemos en la ingeniería de software crítico, donde un solo error puede tener consecuencias catastróficas; en el diseño de nuevos fármacos, donde es vital predecir con exactitud las interacciones moleculares; en la ciencia de materiales, para descubrir compuestos con propiedades deseadas; o en la física teórica, para explorar las complejas implicaciones de nuevas teorías. En todos estos dominios, la capacidad de generar hipótesis creativas y luego someterlas a una verificación rigurosa y automatizada podría acelerar el ritmo del descubrimiento de manera exponencial.
Aristóteles, nombrado en honor al filósofo que sentó las bases de la lógica formal hace más de dos milenios, ha cerrado un círculo histórico. No se ha limitado a resolver algunos de los problemas matemáticos más difíciles del mundo. Nos ha mostrado una nueva forma de razonar, una en la que la creatividad humana y la potencia de la inteligencia artificial no compiten, sino que colaboran. Nos ha ofrecido un primer vistazo a un futuro en el que esta asociación nos permitirá explorar el universo y sus verdades fundamentales con una profundidad y una certeza que nunca antes habíamos imaginado.
Referencias
Luoxin Chen, Jinming Gu, Liankai Huang, Wenhao Huang, Zhicheng Jiang, Allan Jie, Xiaoran Jin, Xing Jin, Chenggang Li, Kaijing Ma, Cheng Ren, Jiawei Shen, Wenlei Shi, Tong Sun, He Sun, Jiahui Wang, Siran Wang, Zhihong Wang, Chenrui Wei, Shufa Wei, Yonghui Wu, Yuchen Wu, Yihang Xia, Huajian Xin, Fan Yang, Huaiyuan Ying, Hongyi Yuan, Zheng Yuan, Tianyang Zhan, Chi Zhang, Yue Zhang, Ge Zhang, Tianyun Zhao, Jianqiu Zhao, Yichi Zhou, and Thomas Hanwen Zhu. Seed-Prover: Deep and Broad Reasoning for Automated Theorem Proving, 2025.
Yuri Chervonyi, Trieu H. Trinh, Miroslav Olšák, Xiaomeng Yang, Hoang Nguyen, Marcelo Menegali, Junehyuk Jung, Vikas Verma, Quoc V. Le, and Thang Luong. Gold-medalist Performance in Solving Olympiad Geometry with AlphaGeometry2, 2025.
Kefan Dong and Tengyu Ma. STP: Self-Play LLM Theorem Provers with Iterative Conjecturing and Proving, 2025.
Google DeepMind. AlphaProof: when reinforcement learning meets formal mathematics. YouTube video, March 2025.
Harmonic. IMO2025: Harmonic’s IMO 2025 Results (Problems & Proofs in Lean). GitHub repository, 2025.
Harmonic. (2025) Aristotle: IMO-level Automated Theorem Proving. Arxiv 2510.01346.
Harmonic. Running Lean at Scale. Blog post, September 11, 2025.
Yong Lin, Shange Tang, Bohan Lyu, Jiayun Wu, Hongzhou Lin, Kaiyu Yang, Jia Li, Mengzhou Xia, Danqi Chen, Sanjeev Arora, and Chi Jin. Goedel-Prover: A Frontier Model for Open-Source Automated Theorem Proving, 2025.
Xiaoyang Liu, Kangjie Bao, Jiashuo Zhang, Yunqi Liu, Yu Chen, Yuntian Liu, Yang Jiao, and Tao Luo. ATLAS: Autoformalizing Theorems through Lifting, Augmentation, and Synthesis of Data, 2025.
Alexander Meiburg. Two lemmas for approxhom. GitHub pull request #251 in teorth/pfr, 2025.
Alexander Meiburg. Roots of Matrix.charpoly are the eigenvalues. GitHub pull request #27118 in leanprover-community/mathlib4, 2025.
Alexander Meiburg. limsup/liminf of when either f or g tends to zero. GitHub pull request #27115 in leanprover-community/mathlib4, 2025.
Alexander Meiburg. Niven’s theorem. GitHub pull request #26371 in leanprover-community/mathlib4, 2025.
Alexander Meiburg, Leonardo A Lessa, and Rodolfo R. Soldati. Quantum information in Lean, 2025.
Azim Ospanov, Farzan Farnia, and Roozbeh Yousefzadeh. APOLLO: Automated LLM and Lean Collaboration for Advanced Formal Reasoning, 2025.
Z. Z. Ren, Zhihong Shao, Junxiao Song, Huajian Xin, Haocheng Wang, Wanjia Zhao, Liyue Zhang, Zhe Fu, Qihao Zhu, Dejian Yang, Z. F. Wu, Zhibin Gou, Shirong Ma, Hongxuan Tang, Yuxuan Liu, Wenjun Gao, Daya Guo, and Chong Ruan. DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition, 2025.
Ziju Shen, Naohao Huang, Fanyi Yang, Yutong Wang, Guoxiong Gao, Tianyi Xu, Jiedong Jiang, Wanyi He, Pu Yang, Mengzhou Sun, Haocheng Ju, Peihao Wu, Bryan Dai, and Bin Dong. REAL-Prover: Retrieval Augmented Lean Prover for Mathematical Reasoning, 2025.
Terence Tao. Some corrections. GitHub pull request #113 in teorth/analysis, 2025.
Terence Tao. Machine-assisted proof. Notices of the American Mathematical Society, 72(1):6-13, 2025.
Haiming Wang, Mert Unsal, Xiaohan Lin, Mantas Baksys, Junqi Liu, Marco Dos Santos, Flood Sung, Marina Vinyes, Zhenzhe Ying, Zekai Zhu, Jianqiao Lu, Hugues de Saxcé, Bolton Bailey, Chendong Song, Chenjun Xiao, Dehao Zhang, Ebony Zhang, Frederick Pu, Han Zhu, Jiawei Liu, Jonas Bayer, Julien Michel, Longhui Yu, Léo Dreyfus-Schmidt, Lewis Tunstall, Luigi Pagani, Moreira Machado, Pauline Bourigault, Ran Wang, Stanislas Polu, Thibaut Barroyer, Wen-Ding Li, Yazhe Niu, Yann Fleureau, Yangyang Hu, Zhouliang Yu, Zihan Wang, Zhilin Yang, Zhengying Liu, and Jia Li. Kimina-Prover Preview: Towards Large Formal Reasoning Models with Reinforcement Learning, 2025.
Huajian Xin, Z. Ren, Z. Junxiao Song, Zhihong Shao, Wanjia Zhao, Haocheng Wang, Bo Liu, Liyue Zhang, Xuan Lu, Qiushi Du, Wenjun Gao, Qihao Zhu, Dejian Yang, Zhibin Gou, F. Wu, Z. Fuli Luo, and Chong Ruan. DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search, 2025.
Ran Xin, Chenguang Xi, Jie Yang, Feng Chen, Hang Wu, Xia Xiao, Yifan Sun, Shen Zheng, and Ming Ding. BFS-Prover: Scalable Best-First Tree Search for LLM-based Automatic Theorem Proving, July 2025.
Zhouliang Yu, Ruotian Peng, Keyi Ding, Yizhe Li, Zhongyuan Peng, Minghao Liu, Yifan Zhang, Zheng Yuan, Huajian Xin, Wenhao Huang, Yandong Wen, Ge Zhang, and Weiyang Liu. FormalMATH: Benchmarking Formal Mathematical Reasoning of Large Language Models, 2025.
Jingyuan Zhang, Qi Wang, Xingguang Ji, Yahui Liu, Yang Yue, Fuzheng Zhang, Di Zhang, Guorui Zhou, and Kun Gai. Lean Abell-Prover: Posttraining Scaling in Formal Reasoning, 2025.
Yichi Zhou, Jianqiu Zhao, Yongxin Zhang, Bohan Wang, Siran Wang, Luoxin Chen, Jiahui Wang, Haowei Chen, Allan Jie, Xinbo Zhang, Haocheng Wang, Luong Trung, Rong Ye, Phan Nhat Hoang, Huishuai Zhang, Peng Sun, and Hang Li. Solving Formal Math Problems by Decomposition and Iterative Reflection, 2025.
Thomas Zhu, Joshua Clune, Jeremy Avigad, Albert Qiaochu Jiang, and Sean Welleck. Premise Selection for a Lean Hammer, 2025.



