En el vasto y a menudo desconcertante universo de las matemáticas y la física, hay preguntas cuya respuesta se ha resistido a generaciones de mentes brillantes, convirtiéndose en auténticos desafíos ancestrales. Una de las más profundas y elusivas es si las ecuaciones que rigen el movimiento de los fluidos, desde las corrientes oceánicas hasta el aire que respiramos, pueden producir singularidades. Piense en un torbellino en un río, en el vapor que se arremolina sobre una taza de té, o en las turbulentas nubes de una tormenta. Estos fenómenos, tan comunes en la vida diaria, están gobernados por leyes matemáticas complejas, pero fundamentales. La gran incógnita es si, bajo ciertas condiciones, estas ecuaciones pueden generar un punto en el espacio y el tiempo donde las propiedades del fluido, como su velocidad o presión, se disparan hacia el infinito. Un evento de esta naturaleza, conocido en el argot científico como blow-up o explosión en tiempo finito, marcaría una frontera en nuestro conocimiento, indicando que nuestras actuales teorías del movimiento de los fluidos no son capaces de describir completamente la realidad en todos los escenarios.
La importancia de este interrogante trasciende la mera curiosidad académica. Las ramificaciones de una respuesta tienen un vasto alcance, impactando campos tan diversos como la ingeniería aeroespacial, la oceanografía, y la climatología. El caso más célebre es el de las ecuaciones de Navier-Stokes, que modelan el flujo de líquidos y gases. La demostración de si estas ecuaciones admiten o no singularidades a partir de condiciones iniciales suaves es tan trascendental que figura como uno de los siete «Problemas del Premio del Milenio» del Instituto de Matemáticas Clay, ofreciendo un premio de un millón de dólares a quien logre resolverlo. Se trata de un desafío que ha perdurado en el tiempo, un recordatorio de que los límites de nuestro saber aún nos guardan grandes sorpresas y que los pilares sobre los que se sustenta la física de la materia aún no han sido completamente afianzados.
Durante mucho tiempo, los intentos por desentrañar este enigma se han apoyado en dos pilares: el análisis matemático puro y las simulaciones computacionales. Históricamente, los enfoques numéricos han identificado principalmente singularidades estables. Una singularidad estable es un resultado robusto; es decir, su formación es predecible incluso si las condiciones iniciales del fluido son alteradas de forma mínima. Piense en la convergencia de varias corrientes de aire en un huracán; es un fenómeno que se mantiene a pesar de las pequeñas variaciones en el sistema. Pero los expertos sospechan que las singularidades que podrían ocurrir en problemas más profundos y fundamentales, como en las ecuaciones de Euler sin límites que describen el flujo de un fluido ideal, son de una naturaleza muy distinta. Se postula que deben ser singularidades inestables.
Una singularidad inestable es, por su propia esencia, extraordinariamente difícil de hallar. Imagine el precario equilibrio de un lápiz sobre su punta perfectamente afilada. Requiere un ajuste infinitamente preciso de sus condiciones iniciales. El más mínimo soplo de aire desvía su trayectoria, provocando su inevitable caída. De manera análoga, una singularidad inestable exige una exactitud milimétrica en las condiciones de arranque del fluido. Cualquier pequeña perturbación desvía la solución de su camino hacia la «explosión». Esta fragilidad inherente ha convertido su descubrimiento sistemático en un reto formidable para los métodos computacionales convencionales. Hasta ahora, la presencia de estas inestabilidades había impedido el uso de técnicas como las simulaciones de avance en el tiempo como base para una construcción matemática rigurosa de la explosión. No obstante, un equipo de científicos ha logrado un hito monumental: el primer hallazgo sistemático de nuevas familias de singularidades inestables. Su trabajo no solo ha revelado la existencia de estos fenómenos esquivos, sino que también ha proporcionado un nuevo «manual de juego» para explorar el vasto y complejo panorama de las ecuaciones diferenciales parciales no lineales, empleando una combinación de inteligencia artificial con herramientas de optimización de alta precisión.
El logro de estos investigadores es un ejemplo elocuente de la sinergia entre el conocimiento matemático profundo y la agilidad de la computación moderna. El equipo ha desarrollado un marco computacional capaz de identificar y resolver estas elusivas soluciones inestables con la exactitud necesaria para un escrutinio matemático riguroso. La piedra angular de su metodología es una reformulación del problema de la dinámica de fluidos en coordenadas autosimilares. Este cambio de perspectiva es brillante. En lugar de la ardua tarea de seguir la evolución de un sistema que cambia rápidamente en el tiempo, la búsqueda se transforma en la de encontrar un perfil estacionario y suave, un retrato del sistema en un punto específico de su evolución. Esta innovadora estrategia permite a las redes neuronales concentrarse en encontrar un perfil de solución constante en el espacio, en vez de uno que se acelera de manera explosiva en el tiempo, haciendo que lo imposible sea, por primera vez, alcanzable. La capacidad de las redes neuronales para aproximar funciones con extrema precisión, combinada con la reformulación del problema, convierte la tarea en una búsqueda de un punto de solución estable en un paisaje computacional, en lugar de un rastro que se desvanece en un espacio de parámetros infinito.
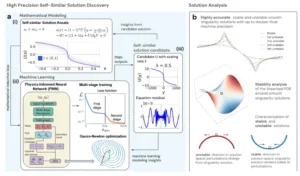
Una sinergia inusual: cuando las matemáticas se fusionan con el aprendizaje automático
El núcleo de este avance sin precedentes reside en una metodología innovadora que entrelaza la potencia del aprendizaje automático con el rigor inflexible del análisis matemático. Los autores del estudio modelaron sus soluciones utilizando redes neuronales informadas por la física (PINNs), un tipo de inteligencia artificial que ha emergido como una herramienta prometedora para resolver ecuaciones diferenciales. A diferencia de los modelos de IA tradicionales, que se alimentan de vastas cantidades de datos para aprender patrones, las PINNs están diseñadas con la física y la matemática del problema ya incorporadas. Su principal objetivo no es la velocidad o la eficiencia, sino la calidad y la precisión de las soluciones descubiertas, lo que permite abordar problemas para los cuales los datos son escasos o simplemente inexistentes, como es el caso de estas raras singularidades.
Las PINNs funcionan minimizando una función de pérdida que incluye no solo el cumplimiento de las condiciones de contorno, sino también la satisfacción de las propias ecuaciones que rigen el fenómeno. En este caso particular, el desafío era encontrar las esquivas singularidades inestables, algo que las simulaciones numéricas clásicas habían fracasado en capturar debido a su extrema sensibilidad a las perturbaciones. El equipo de investigación superó las limitaciones inherentes de las PINNs, que habitualmente no alcanzan la precisión requerida para una prueba matemática formal, con una estrategia de doble enfoque que elevó el nivel de la computación científica a una nueva altura.
En primer lugar, los científicos incorporaron una estructura matemática intrínseca en la red neuronal. En lugar de permitir que la red aprendiera la solución de forma independiente, sus arquitecturas integran de manera directa las propiedades físicas y matemáticas conocidas de las soluciones. Esto incluye simetrías, la periodicidad de las ondas y el comportamiento asintótico en los extremos del dominio. Al incorporar estas «ventajas inductivas» en el diseño de la red, se guía el proceso de optimización hacia resultados que tienen sentido físico y matemático, evitando las respuestas triviales o erróneas. Los investigadores manejaron dominios infinitos, una característica crucial de estos problemas autosimilares, mediante transformaciones de coordenadas que compactan el espacio, permitiendo que la red operara en un dominio finito y normalizado. Adicionalmente, para imponer comportamientos asintóticos precisos en el origen o en el infinito, utilizaron «envolventes de solución», que son factores multiplicativos que fuerzan a la salida de la red a decaer de la manera correcta. Esta estrategia alivia la carga del optimizador, que en lugar de aprender las restricciones globales, se concentra en capturar los detalles localizados de la solución.
El segundo pilar de su éxito es un esquema de entrenamiento de altísima precisión. Los métodos de optimización convencionales, como el ubicuo algoritmo Adam, resultaron insuficientes para producir soluciones de la calidad requerida para las ecuaciones autosimilares. En su lugar, el equipo adoptó un enfoque de Gauss-Newton de matriz completa. Aunque esta metodología es computacionalmente intensiva, es capaz de refinar la solución de manera mucho más efectiva y de lograr una convergencia significativamente más rápida que los métodos estándar. La viabilidad de este enfoque se debe al tamaño relativamente modesto de las redes neuronales utilizadas, lo que compensa su alto costo computacional. Para alcanzar un nivel de exactitud sin precedentes, los investigadores desarrollaron un esquema de entrenamiento por etapas múltiples. En este proceso, una primera red se entrena hasta un cierto nivel de precisión. Luego, una segunda red, nueva y especializada, se entrena para corregir los pequeños errores residuales de la primera. La salida final se obtiene combinando los resultados de ambas redes. Esta sofisticada técnica es tan efectiva que, para algunas soluciones, como las de las ecuaciones de Córdoba-Córdoba-Fontelos (CCF), el equipo logró mejorar los residuos máximos en cinco órdenes de magnitud, alcanzando una exactitud asombrosa de . Este nivel de precisión no es solo un logro técnico; es el requisito mínimo para la validación asistida por computadora (CAP), un paso crucial para la certificación formal de estas soluciones en el ámbito de la matemática pura.
Un nuevo mapa de la inestabilidad
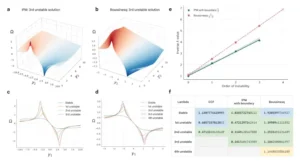
El marco computacional desarrollado por los científicos les ha permitido desvelar un tesoro de nuevas soluciones para sistemas de fluidos fundamentales: las ecuaciones CCF, la ecuación de medio poroso incompresible (IPM) y las ecuaciones de Boussinesq. En el caso de las ecuaciones de Boussinesq, que en presencia de un contorno son análogas a las ecuaciones de Euler tridimensionales con contornos, los investigadores no solo confirmaron la solución estable, sino que descubrieron tres singularidades inestables distintas, además de una cuarta candidata. Este es el primer descubrimiento de cualquier solución autosimilar inestable y suave para una ecuación de fluidos incompresibles no forzada que conduzca a una singularidad en tiempo finito. El hito es de una magnitud que redefine el panorama del campo.
Cada solución descubierta se caracteriza por un parámetro de escala, denotado por . De forma fascinante, los investigadores observaron una relación empírica simple entre este parámetro y el grado de inestabilidad de la solución. Por ejemplo, para las ecuaciones de Boussinesq, encontraron que el valor de para la n-ésima singularidad inestable se aproxima a la fórmula . Un patrón similar emergió para las soluciones de las ecuaciones IPM. En términos sencillos, un valor menor de corresponde a una solución más inestable y a una singularidad más severa, con una tasa de explosión más rápida. Estas fórmulas asintóticas no son solo una revelación curiosa, sino una herramienta práctica inestimable: proporcionan valores iniciales de alta calidad para futuros estudios, lo que facilita el descubrimiento de nuevas soluciones y acelera la convergencia de los algoritmos de optimización.
Para validar la admisibilidad de los valores de , los autores idearon una técnica ingeniosa. Argumentaron que solo los valores de que son «correctos» o físicamente válidos admiten soluciones suaves, lo que se traduce en que el error residual de la ecuación debe ser mínimo. Al entrenar la red para diferentes valores de y evaluar el residuo máximo de la ecuación, encontraron que el error forma una curva con una forma de embudo o un «cuenco», con el valor óptimo en la parte más baja. La estrechez de este «cuenco» numérico les permitió determinar con seguridad cuántos dígitos significativos de la solución son válidos, estableciendo un método riguroso para la validación numérica. Este enfoque es tan preciso que, en el caso de la solución de las ecuaciones IPM, el equipo pudo determinar el valor de con dieciséis dígitos de precisión, una hazaña asombrosa que supera con creces los trabajos anteriores.
Profundizando en los fundamentos: la ciencia detrás del descubrimiento
Para comprender plenamente la trascendencia de este trabajo, es crucial ahondar en la naturaleza de los problemas que los científicos han abordado y en los conceptos matemáticos que han explotado. Las ecuaciones de Navier-Stokes y de Euler, a pesar de su aparente simplicidad, representan un desafío matemático formidable. Su naturaleza no lineal es la raíz de su complejidad. Una ecuación lineal es como una simple suma: si conocemos la respuesta para A y para B, la respuesta para A+B es simplemente la suma de las respuestas individuales. En una ecuación no lineal, como las que gobiernan los fluidos, las interacciones entre las partes del sistema no se suman de manera simple. La respuesta de A+B no es predecible a partir de las respuestas de A y B por separado. Es esta falta de predictibilidad la que puede dar lugar a fenómenos inesperados como la turbulencia o, en el peor de los casos, a las explosiones.
El equipo se centró en un tipo particular de solución conocida como soluciones autosimilares. Este es un concepto clave y digno de ser explicado. Una solución autosimilar es una que se ve idéntica a sí misma si se mira a diferentes escalas, es decir, si se le hace un «zoom in» o «zoom out» en el tiempo y el espacio. La forma de un fenómeno autosimilar permanece constante, mientras su tamaño aumenta o disminuye. Piensen en un remolino de humo que se expande, pero cuya forma y estructura interna no cambian. Al redefinir el problema de la singularidad en términos de un perfil autosimilar estacionario, los investigadores transformaron una búsqueda imposible, la de un punto en el espacio-tiempo que se acelera hasta el infinito, en una mucho más manejable: la de un perfil de solución constante en un dominio espacial compacto. Este cambio de coordenadas es la base de su éxito, ya que permite que las redes neuronales, que son por naturaleza excelentes aproximadoras de funciones continuas y suaves, trabajen en un espacio donde no hay «explosiones» que las confundan. La búsqueda se convierte entonces en un problema de optimización, donde la red busca la forma de función que minimiza el error de la ecuación, es decir, que mejor la satisface.
La elección de las ecuaciones CCF, IPM y Boussinesq como bancos de prueba tampoco es casual. Estas ecuaciones son modelos simplificados o análogos de las ecuaciones de Euler tridimensionales, el verdadero «santo grial» de la física de fluidos. La ecuación CCF, por ejemplo, modela una singularidad que ocurre en el eje de simetría de un fluido. Las ecuaciones IPM describen la evolución de la interfaz de un fluido con otro, un modelo relevante en aplicaciones como la inyección de fluidos en suelos porosos. Y las ecuaciones de Boussinesq, que modelan el flujo de un fluido con densidad variable, son de gran relevancia en la meteorología y la oceanografía. Al demostrar que su método funciona en estos sistemas análogos, los científicos han validado su enfoque para el problema de las singularidades de manera general, pavimentando el camino para futuras investigaciones en los sistemas más complejos.
Además, el método de validación numérica basado en el «cuenco de error» es una contribución metodológica de gran valor. En el mundo de la computación científica, una solución numérica no es una prueba matemática, ya que la precisión siempre está limitada por el poder de cálculo y los errores de redondeo. Sin embargo, al demostrar que la precisión de la solución de la red neuronal es máxima solo para valores de que son matemáticamente «correctos», los investigadores establecieron una conexión directa entre el resultado computacional y la validez matemática. Este enfoque va más allá de un simple cálculo. Es una forma de argumentar a favor de la existencia de una solución a partir de evidencia numérica, lo que abre un camino viable para la demostración asistida por computadora en problemas que son demasiado complejos para el análisis humano.
Conclusiones y un nuevo horizonte para la ciencia de fluidos
Este estudio no solo ha resuelto algunas preguntas, sino que ha abierto la puerta a una nueva generación de desafíos y exploraciones. El principal es aplicar esta misma metodología a las ecuaciones de Euler sin límites, un problema aún más formidable por la ausencia de contornos que puedan «estabilizar» las soluciones. Para lograrlo, será necesario profundizar en nuestra comprensión de las propiedades cualitativas de estas soluciones y utilizar ese conocimiento para refinar aún más el diseño de las arquitecturas de PINN y los métodos de entrenamiento. La investigación de la estructura topológica de los fluidos, la forma de los torbellinos y los filamentos de vorticidad, será clave para alimentar a los modelos de IA con la información necesaria para encontrar las soluciones.
La búsqueda de las singularidades fluidas es un viaje épico. Si bien este estudio no ha resuelto el problema del milenio de Navier-Stokes, ha proporcionado un mapa detallado y un conjunto de herramientas de última generación para la expedición. La habilidad para descubrir y caracterizar singularidades inestables es un paso crucial hacia la comprensión de estos fenómenos fundamentales. Al revelar la «danza» oculta de la inestabilidad en los fluidos, este trabajo nos acerca a la resolución de uno de los misterios más profundos y longevos de la física matemática.
Desde una perspectiva más amplia, la investigación tiene implicaciones de gran calado para el futuro de la ciencia. Demuestra que la inteligencia artificial no es solo una herramienta para procesar datos, sino un socio en el proceso de descubrimiento. Al complementar la intuición humana y el razonamiento deductivo con la capacidad de las redes neuronales para explorar vastos espacios de soluciones, estamos desbloqueando un potencial sin precedentes para resolver problemas científicos que han permanecido inamovibles durante décadas. La intersección de las matemáticas, la física y el aprendizaje automático está creando un nuevo paradigma en la investigación, en el que los límites entre lo teórico y lo computacional se desdibujan cada vez más. El uso de la IA para generar hipótesis y para encontrar soluciones a problemas que escapan a la intuición humana no es una fantasía de ciencia ficción, sino una realidad palpable que ha encontrado un éxito notable en este campo. La posibilidad de utilizar máquinas para descubrir nuevas leyes físicas o para validar teoremas matemáticos de manera formal está más cerca que nunca.
La ciencia, en su esencia, es un ejercicio de descubrimiento y de construcción de conocimiento. A lo largo de la historia, hemos utilizado telescopios para ver galaxias lejanas, microscopios para observar células minúsculas, y aceleradores de partículas para estudiar la materia en su nivel más fundamental. Cada nueva herramienta nos ha permitido ver un aspecto de la realidad que antes nos era inaccesible. Las redes neuronales informadas por la física son una de estas nuevas herramientas. Son un «ojo» que nos permite ver la forma de las soluciones matemáticas, que de otra manera permanecerían ocultas en la inmensidad de las ecuaciones.
La relevancia social de este trabajo no es menos significativa. La física de fluidos tiene un impacto directo en nuestra vida cotidiana. Entender la turbulencia es fundamental para el diseño de aeronaves más eficientes, para la predicción de huracanes más precisas, y para el desarrollo de tecnologías de energía renovable, como las turbinas eólicas. El descubrimiento de estas singularidades, y los métodos para encontrarlas, nos da una nueva base teórica para comprender y, en última instancia, controlar, los flujos complejos en la naturaleza y en la ingeniería.
En la búsqueda de la verdad, el camino es a menudo tan importante como el destino. Si bien este estudio no ha resuelto el problema del milenio de Navier-Stokes, ha proporcionado un mapa detallado y un conjunto de herramientas de última generación para la expedición. Nos ha mostrado que incluso los enigmas más antiguos pueden ceder ante un enfoque innovador, y que las respuestas a los grandes misterios a menudo residen en la intersección de la tradición y la innovación. El hallazgo de estas singulares y elusivas soluciones inestables es un triunfo del ingenio humano, un recordatorio de que, incluso en un mundo lleno de datos, los descubrimientos más importantes provienen de la formulación de las preguntas correctas.
Referencias
- Wang, Y., Bennani, M., Martens, J., Racanière, S., Blackwell, S., Matthews, A., Nikolov, S., Cao-Labora, G., Park, D. S., Arjovsky, M., Worrall, D., Qin, C., Alet, F., Kozlovskii, B., Tomašev, N., Davies, A., Kohli, P., Buckmaster, T., Georgiev, B., Gómez-Serrano, J., Jiang, R., & Lai, C.-Y. (2025). Discovery of Unstable Singularities. arXiv preprint arXiv:2509.14185.
- Wang, Y., Liu, Z., Li, Z., Anandkumar, A., & Hou, T. Y. (2025). High precision PINNs in unbounded domains: application to singularity formulation in PDEs. arXiv preprint arXiv:2506.19243.
- Raissi, M., Perdikaris, P., & Karniadakis, G. (2019). Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys., 378, 686-707.
- Karniadakis, G. E., et al. (2021). Physics-informed machine learning. Nat. Rev. Phys., 3, 422-440.
- Gómez-Serrano, J. (2019). Computer-assisted proofs in PDE: a survey. SeMA J., 76, 459-484.
- Luo, G., & Hou, T. Y. (2014). Potentially singular solutions of the 3D axisymmetric Euler equations. Proc. Natl. Acad. Sci., 111, 12968-12973.
- Eggers, J., & Fontelos, M. A. (2009). The role of self-similarity in singularities of partial differential equations. Nonlinearity, 22, R1-R44.
- Hou, T. Y. (2009). Blow-up or no blow-up? A unified computational and analytic approach to 3D incompressible Euler and Navier-Stokes equations. Acta Numer., 18, 277-346.
- Fefferman, C. L. (2000). Existence and smoothness of the Navier-Stokes equation. The Millennium Prize Problems, 57, 67.
- Smale, S. (1998). Mathematical problems for the next century. Math. Intell., 20, 7-15.
- Wang, Y., & Lai, C.-Y. (2024). Multi-stage neural networks: function approximator of machine precision. J. Comput. Phys., 504, 112865.
- Martens, J. (2020). New insights and perspectives on the natural gradient method. J. Mach. Learn. Res., 21, 1-76.